Значения обратных тригонометрических функций y=arcsin(x) и y=arccos(x)

 Вычислим угол \(\alpha\) на  промежутке \([ -\frac{\pi }{2};\frac{\pi }{2}]\) , так как функция \(y=arcsin(x)\) обратная для функции \(y=sin(x)\) на отрезке \(y ∈[ − π / 2 , π / 2 ] \), где \(x ∈ [ − 1 , 1 ] \).

Рассмотрим угол \( \sin \alpha =-\frac{\sqrt{3}}{2}\) . Нарисуем на оси \(oy\) значение \(-\frac{\sqrt{3}}{2}\). \(-\frac{\sqrt{3}}{2}\) соответствует \({{\alpha }_{1}}=-\frac{\pi }{3}\) и \({{\alpha }_{2}}=-\frac{2\pi }{3}\), но промежуток \(\left[ -\frac{\pi }{2};\frac{\pi }{2} \right]\) включает только \({{\alpha }_{1}}=-\frac{\pi }{3}\). Вывод: \(\arcsin \left( -\frac{\sqrt{3}}{2} \right)=-\frac{\pi }{3}\).

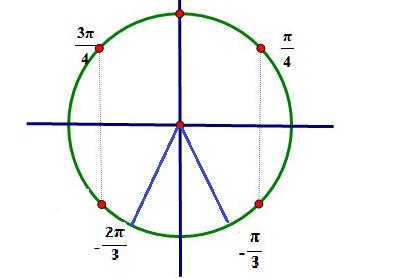
Функция арксинус нечетная, тогда \(\arcsin \left( -\frac{\sqrt{3}}{2} \right)=-\arcsin \frac{\sqrt{3}}{2}\).  \(\arcsin \frac{\sqrt{3}}{2}\) найдем, используя таблицу значений \(\sin \alpha =\frac{\sqrt{3}}{2} \) при \(\alpha =\frac{\pi }{3}\). Тогда окончательно имеем \( \arcsin \left( -\frac{\sqrt{3}}{2} \right)=-\frac{\pi }{3}\).

Часто задаваемые вопросы: