Обратные тригонометрические функции

Дарим в подарок бесплатный вводный урок!

Предметы

Специализации

Обратные тригонометрические функции принято называть с помощью префикса $arc$ ($arc$ с английского дуга), например, $arcsin (x)$, $arccos(x)$, $arctan(x)$ и т. д. При измерении в радианах угол радиан будет соответствовать дуге, длина которой равна $R$, где $R$-радиус окружности.

Таким образом, в единичной окружности "дуга, косинус которой равен x", совпадает с "углом, косинус которого равен $x$", поскольку длина дуги окружности в радиусах совпадает с измерением угла в радианах. Обозначения $sin-1 (x)$, $cos−1(x)$, $tan−1(x)$ и др. было введено Джоном Гершелем в $1813$ году.

Графики обратных тригонометрических функций (графики аркфункий)

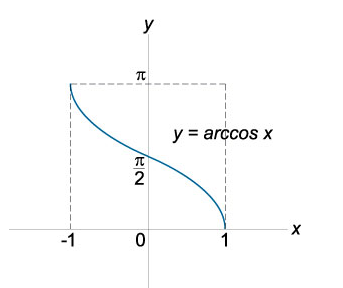
Функция $$y=arccos(x)$ обратная для функции $y=cos(x)$ на отрезке$ $y ∈ [ 0 , π] $ $, где $x ∈ [ − 1 , 1 ]$.$

График арккосинуса:

​

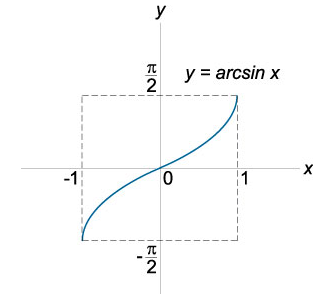
Функция $$y=arcsin(x)$ обратная для функции $y=sin(x)$ на отрезке$ $y ∈[ − π / 2 , π / 2 ] $ $, где $x ∈ [ − 1 , 1 ] $$ .

График арксинуса:

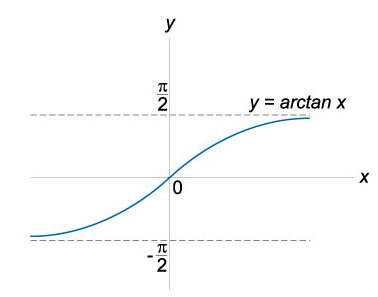
$Функция $y=arctg(x)$ обратная для функции $y=tg(x)$ на отрезке от $[\frac{-\pi}{2}]$ до $[\frac{\pi}{2}]$, где $y ∈ ( − π / 2 , π / 2 ) $.$

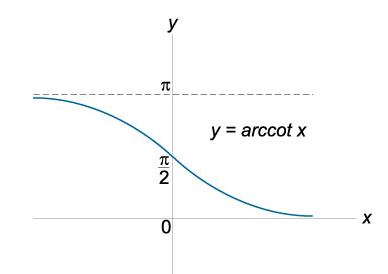
$Функция $y=arcctg(x)$ обратная для функции $y=ctg(x)$ на отрезке от $[\frac{-\pi}{2}]$ до $[\frac{\pi}{2}]$, где $y ∈ ( − π / 2 , π / 2 ) $.$

​

Часто задаваемые вопросы:

✅ Какие значения принимают обратные тригонометрические функции?

↪ Обратные тригонометрические функции возвращают значения углов в интервале [-π/2, π/2] для arcsin и [-π, π] для arccos и arctan.

✅ Как выразить обратные тригонометрические функции через тригонометрические значения?

↪ Например, arcsin(y) можно выразить как sin^-1(y), а arccos(y) как cos^-1(y).

✅ Где применяются обратные тригонометрические функции?

↪ Обратные тригонометрические функции используются в математике, физике, инженерии, компьютерной графике и других областях для решения задач, связанных с углами и тригонометрией.

Больше уроков и заданий по всем школьным предметам в онлайн-школе "Альфа". Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Ольга Викторовна Смольская

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный университет

Проведенных занятий:

1077

Форма обучения:

Дистанционно (Скайп)

Татьяна Дмитриевна Макарова

Репетитор по математике

Стаж (лет)

Образование:

Белорусский государственный педагогический университ имени Максима Танка

Проведенных занятий:

317

Форма обучения:

Дистанционно (Скайп)

Евгений Геннадьевич Горшков

Репетитор по математике

Стаж (лет)

Образование:

Орский государственный педагогический институт им. Т. Г. Шевченко, физико-математический факультет

Проведенных занятий:

233

Форма обучения:

Дистанционно (Скайп)