Определенный интеграл

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

25 янв 2024

Определенный интеграл

Функция определенного интеграла тесно связана с первообразной и неопределенным интегралом функции. Основное отличие состоит в том, что неопределенный интеграл, если он существует, то есть входит в область определения подынтегральной функции, является вещественным числовым значением, в то время как первообразная и неопределенный интеграл представляют собой бесконечное число функций, отличающихся только константой. Развитие определенного интеграла начинается с функции \(f( x) \) на замкнутом интервале \([ a, b]\). Данный интервал разбивается на ” \(n\) " подинтервалов, которые могут, хоть и не обязательно, быть равными длинами \((Δ x)\). В каждом подинтервале выбирается произвольное значение интервала и определяется его последующее значение функции. Произведение каждого значения функции умножается на соответствующую длину подинтервала и эти ” \(n\)" продуктов добавляются для определения их суммы. Эти суммы называются суммами Римана и могут быть положительными, отрицательными или нулевыми в зависимости от поведения функции на замкнутом интервале.

Определенный интеграл имеет вид:

\(\int\limits_a^b f (x)dx\)

область между функцией \(f (x)\) и осью \(x\), где \(x\) колеблется от \(a\) до \(b\). Если

\(F'(x)=f (x)\)

определенный интеграл можно вычислить по формуле "Ньютона-Лейбница":

\(\int\limits_a^b f(x)dx=F(b)-F(a)\)

Нижний предел интегрирования стандартно обозначается буквой \(a\).
Верхний предел интегрирования стандартно обозначается буквой \(b\).
Отрезок \([a, b] \) называется отрезком интегрирования.

Вычислить определенный интеграл от функции значит вычислить все первообразные функции на \(F(b)\) и вычесть значение \(F(а)\) от этого. Это будет равно площади под функцией \([a, b] \).

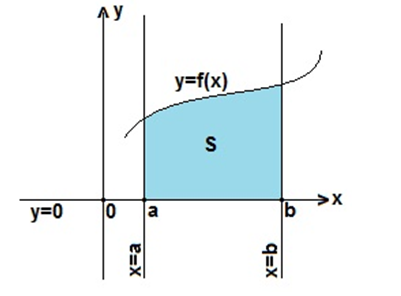
Определенный интеграл не всгда существует, так отрезок интегрирования \([a, b] \) должен входить в область определения подынтегральной функции.

Определенный интеграл можно рассматривать как сумму Римана бесконечно малых прямоугольников:

\(\lim_{n\to\infty}\sum_{i=1}^n f(x_i)\Delta x_i\).

Коэффициент можно выносить за знак интеграла .Если \(f (x) \) константа, то определенный интеграл :

\(\int\limits_a^b k dx = k \int\limits_a^b 1 dx = k(b-a)\)

Определенные интегралы применяются в геометрии, физике и других областях. Например, скорость - это интегралом ускорения. С помощью интегралов можно вычислить объем твердого объекта, например, тела вращения или пирамиды.

Площадь под Кривой
Определенный интеграл на \([А,B]\) равен площади между кривой и осью \(x\). Например, чтобы вычислить площадь под графиком \(f (x)=\sqrt{x}\) на интервале \([0,4]\), сначала возьмем интеграл следующим образом:

\(\int\limits_0^4\sqrt{x}dx=\int\limits_0^4 x^{\frac{1}{2}}dx=\dfrac{2}{3}(4)^{\frac{3}{2}}-\frac{2}{3}(0)^{\frac{3}{2}}=\frac{2}{3}(8)-0=\frac{16}{3}\)

Пример вычислить интеграл \(\int\limits_0^1(x+1)^4dx:\)

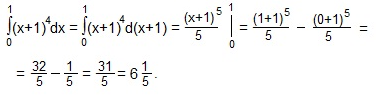
Объем тела вращения

Объем тела вращения вычисляеся по формуле:

\(V=\pi \int\limits_a^b f^2(x) dx \)

Предположим, мы хотим найти объем конуса с радиусом \(R\) и высотой \(h\). Мы можем сделать это путем интеграции круглых сечений от \(0\) до \(h\) . Радиус будет равен расстоянию между осью \(X\) и функции \(y=r-\frac{r}{h}x\) , так что площадь поперечного сечения будет равна \(\pi\left(r-\frac{r}{h}x\right)^2 \) или \(\pi\left(r^2-\frac{2r^2}{h}x+\frac{r^2}{h^2}x^2\right)\) . Поэтому объем конуса будет равен:

\(\begin{align}&\int\limits_0^h\pi\left(r^2-\dfrac{2r^2}{h}x+\frac{r^2}{h^2}x^2\right)dx=\pi\int\limits_0^h\left(r^2-\frac{2r^2}{h}x+\frac{r^2}{h^2}x^2\right)dx =\pi\left(r^2x-\frac{r^2}{h}x^2+\frac{r^2}{3h^2}x^3\right)\bigg|^h_0 \\&=\pi\left(\left(r^2(h)-\frac{r^2}{h}(h)^2+\frac{r^2}{3h^2}(h)^3\right)-\left(r^2(0)-\frac{r^2}{h}(0)^2+\frac{r^2}{3h^2}(0)^3\right)\right) =\pi\left(r^2h-r^2h+\frac{r^2h}{3}-0\right)=\frac{\pi}{3}r^2h\end{align}\)

Область с полярными координатами
Учитывая полярную функцию \(r (\theta)\)), площадь под функцией как сумма Римана равна

\(\lim_{n\to\infty}\sum_{i=1}^n\dfrac{1}{2}r(\theta_i)^2\Delta\theta_i\)

\(\dfrac{1}{2}\int\limits_{\alpha}^{\beta}r(\theta)^2d\theta\)

Длина дуги

Длина дуги может быть вычислена путем суммирования бесконечного числа бесконечно малых отрезков вдоль Кривой:

\(\int\limits_a^b\sqrt{1+\left(\dfrac{dy}{dx}\right)^2}dx\)
Параметрическим уравнение:

\(\int\limits_a^b\sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2} dt\)
В полярных координатах, длина дуги равна
\(\int\limits_{\alpha}^{\beta}\sqrt{r'(\theta)^2+r(\theta)^2}d\theta\)

Предыдущая статья