Как сокращать дроби
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор для подготовки к ОГЭ по физике
- Репетитор по грамматике русского языка
- Английский язык для начинающих
- Репетитор по разговорному английскому
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по информатике для подготовки к ОГЭ
- Подготовка к ОГЭ по литературе
- Программирование Pascal
Сокращение дробей - это процесс упрощения дроби до ее наименьшего возможного выражения. Давайте разберемся, как сокращать дроби шаг за шагом.
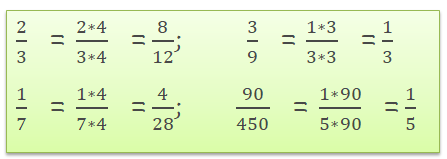
Пошаговое руководство
Шаг 1: Найдите наибольший общий делитель (НОД) числителя и знаменателя дроби. НОД - это наибольшее число, которое делит и числитель, и знаменатель без остатка.
Шаг 2: Разделите числитель и знаменатель дроби на найденный НОД. Это позволит упростить дробь до наименьшего возможного выражения.
Пример: Допустим, у нас есть дробь 8/12, и мы хотим ее сократить.
Решение:
Шаг 1: Найдем НОД числителя 8 и знаменателя 12. В данном случае НОД равен 4.
Шаг 2: Разделим числитель 8 и знаменатель 12 на 4: 8 ÷ 4 = 2 12 ÷ 4 = 3
Ответ: Сокращенная форма дроби 8/12 равна 2/3.
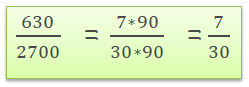
Часто задаваемые вопросы:
✅ Что такое наибольший общий делитель (НОД)?
↪ Наибольший общий делитель (НОД) - это наибольшее число, которое одновременно делит без остатка два или более числа. НОД используется в математике для сокращения дробей и выполнения других операций.
↪ Сокращение дробей имеет несколько практических преимуществ. Во-первых, сокращенные дроби более компактны и удобны для работы. Они помогают упростить вычисления и анализ математических задач. Во-вторых, сокращение дробей позволяет найти их наименьшее общее выражение и представить в более простой форме.
✅ Как можно найти наибольший общий делитель (НОД) чисел?
↪ Существуют различные методы для нахождения НОД чисел. Некоторые из них включают использование алгоритма Евклида, факторизацию чисел и поиск общих делителей. Алгоритм Евклида является одним из наиболее эффективных и широко используемых методов для нахождения НОД. Он основан на последовательных делениях чисел и нахождении остатков.
- Признак делимости на 23
- МИФИ: Прикладная математика и физика
- Задача на растворы
- Как по заданным функции, точке и вектору вычислить градиент в точке и производную функции в точке по направлению вектора
- Задачи с прикладным содержанием (вариант 3)
- Решаем олимпиадные задачи для 2 класса
- Выпускной-2021: актуальные образы для 9-классников
- Если мамы нет дома: готовим простые и вкусные перекусы