Площадь трапеции

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Немного истории
Основные формулы
Часто задаваемые вопросы

18 апр 2024

Площадь трапеции

Немного истории

Для начала вспомним, что такое трапеция.

Трапеция – это фигура, у которой две стороны параллельны, а две другие не параллельны.

Трапеция – одна из самых «загадочных» фигур школьной планиметрии. Она обладает некоторыми признаками параллелограмма, но сильно отличается от него разнообразием форм. Различают трапеции прямоугольные, равнобедренные, общего вида. Одно это разнообразие форм уже подозрительно.

На практике форма трапеции встречается более часто, чем прямоугольники, квадраты или параллелограммы. Поэтому нахождение площади для трапеции – более актуальная задача, чем для других фигур.

Покажем вам несколько формул, как найти площадь трапеции. Каждая формула площади трапеции подходит для решения соответствующего круга задач.

Основные формулы

Площадь трапеции через её основания и высоту:

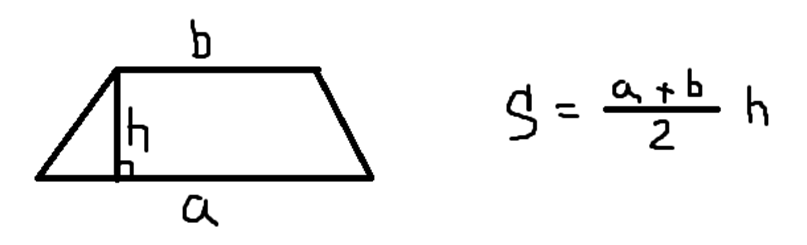
Площадь трапеции через ее высоту и среднюю линию:

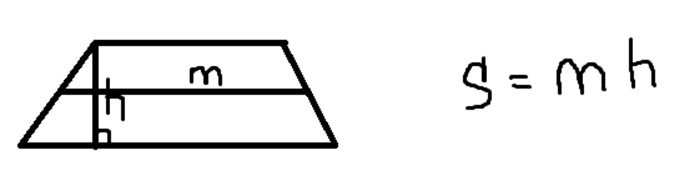
Площадь трапеции через ее диагонали и угол между ними:

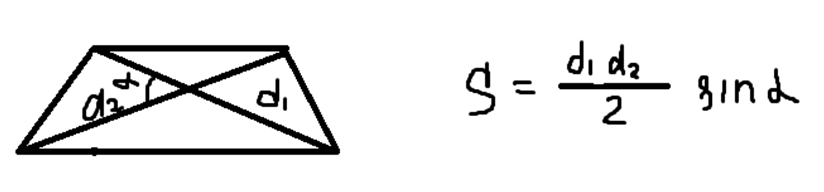
Давайте разберем задачу, иллюстрирующую применение одной из этих формул:

Задача

Основания трапеции общего вида равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

Решение

Изобразим трапецию общего вида и введём обозначения, как показано на рисунке ниже.

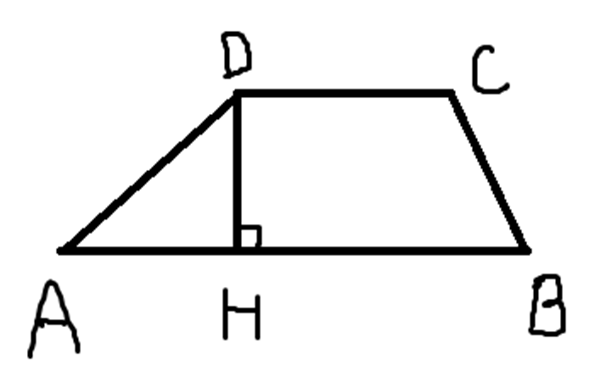
По условию задачи, один из углов трапеции равен 150°. Этим углом может быть угол ADC. По свойству трапеции, также как и параллелограмма, сумма углов, прилежащих к боковой стороне, равна 180°. Отсюда несложно вычислить, что второй угол, DAН, прилежащий к этой боковой стороне, будет равен 30°.

Отрезком DH на рисунке является высота трапеции. Найдем эту высоту из прямоугольного треугольника AHD, где DH является противолежащим катетом, AD является гипотенузой:

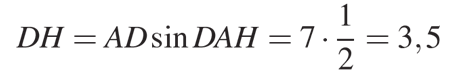
Воспользуемся формулой (1) площади трапеции через ее основания и высоту. По этой формуле площадь трапеции равна произведению полусуммы оснований на ее высоту:

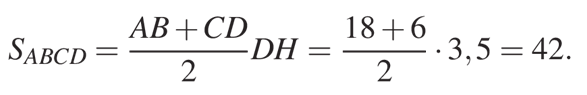
Ответ: 42

Итак, зная длины двух оснований трапеции и ее высоту, вычислить ее площадь достаточно просто. Сложности могут быть, если нам не известны один из требуемых элементов, например, высота трапеции. Но здесь на помощь приходят знания свойств трапеций и соотношений в прямоугольном треугольнике.

Часто задаваемые вопросы

✅ Что такое трапеция?

↪ Трапеция - это четырехугольник, у которого две противоположные стороны параллельны, а две другие стороны непараллельны.

✅ Как найти площадь трапеции?

↪ Площадь трапеции можно найти по формуле: S = (a + b) * h / 2, где a и b - длины оснований трапеции, а h - высота трапеции, опущенная на основание.

✅ Что происходит с площадью трапеции, если увеличить одно из оснований?

↪ Если увеличить одно из оснований трапеции, то ее площадь увеличится, при этом высота трапеции останется неизменной. Если увеличить оба основания на одинаковую величину, то площадь трапеции увеличится в два раза.

Предыдущая статья