Теорема косинусов

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Утверждения, эквивалентные Теореме косинусов, опубликовал в свое время Евклид в своих "Началах". Поэтому считается, что это классика евклидовой геометрии.

Теорема косинусов может быть полезна для решения различных задач, связанных с треугольниками. Она позволяет нам находить длины сторон треугольника, если известны углы и длины других сторон, или находить меры углов, если известны длины сторон.

Теорема косинусов звучит так:

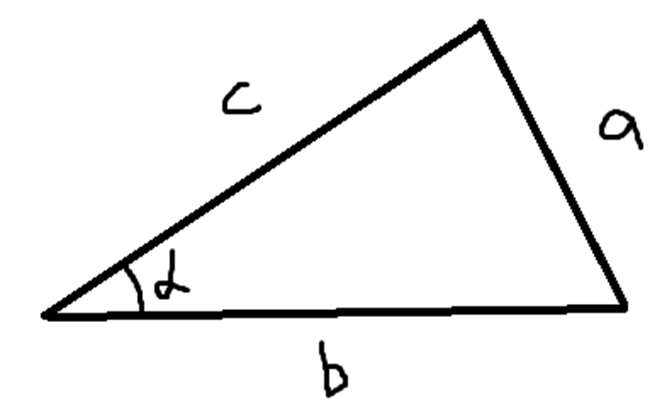
Для плоского треугольника (см. рисунок ниже), у которого обозначены стороны a, b, c и угол α, который противолежит стороне a,

справедливо соотношение: a² = b² + c² – 2bc cosα.

Теорема косинусов — более универсальное соотношение, которое обобщает теорему Пифагора. Если теорема Пифагора справедлива только для прямоугольных треугольников, то теорема косинусов справедлива для любых плоских треугольников. И это очень важное преимущество.

Также удобно, что с помощью Теоремы косинусов можно найти любую сторону треугольника, зная две других и величину угла между ними.

Теорема косинусов имеет два важных следствия:

Теорема косинусов может быть использована для нахождения косинуса угла треугольника, если известны все три стороны (см. рисунок):

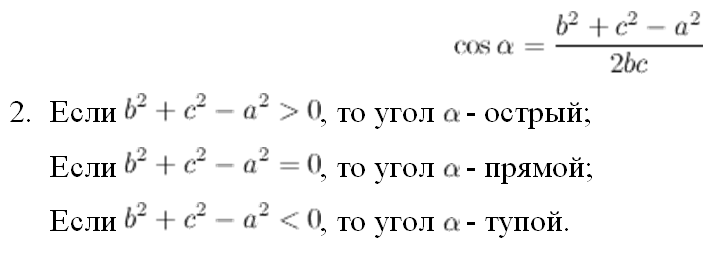
Задачи, в которых используется теорема косинусов, имеют весьма разнообразную тематику. Давайте разберем одну из них.

Задача

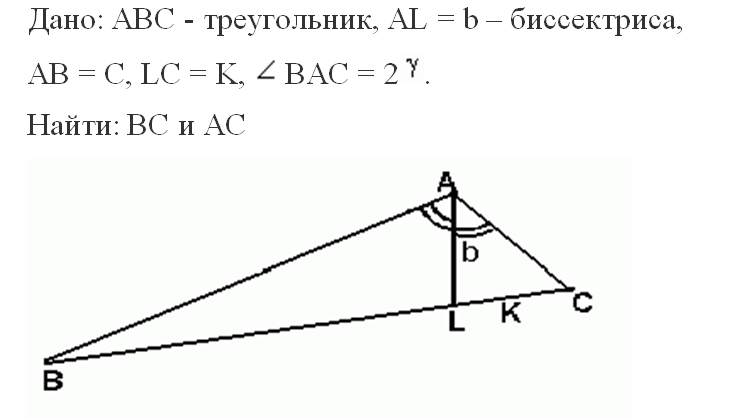
Решение:

Нахождение двух сторон в произвольном треугольнике, если знаем только третью сторону – задача трудная. В этом случае мы использовали свойства биссектрисы делить угол пополам и теорему косинусов. Необходимо было увидеть, что биссектриса не только делит угол пополам, но и образует еще два треугольника, которые нам и помогли решить эту задачу.

Автор - Андрей Найденов

Часто задаваемые вопросы:

Часто задаваемые вопросы

Что такое теорема косинусов?

Теорема косинусов - это математическая формула, которая связывает длины сторон треугольника с мерами его углов.

Как использовать теорему косинусов для вычисления длин сторон треугольника?

Для вычисления длины одной из сторон треугольника с использованием теоремы косинусов, необходимо знать длины двух других сторон и меру включенного угла. Подставив значения в соответствующую формулу, можно вычислить длину третьей стороны.

Как использовать теорему косинусов для вычисления мер углов треугольника?

Теорему косинусов можно использовать для вычисления мер углов треугольника, если известны длины его сторон. Подставив значения в формулы для косинусов углов, можно найти их меры.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

Теорема косинусов

Часто задаваемые вопросы

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи