ЕГЭ по математике, профильный уровень. Задача с параметром

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Обновлено: 14 апр 2024

ЕГЭ по математике, профильный уровень. Задача с параметром

В этой статье преподаватель математики Андрей Алексеевич рассматривает очень непростое, но и очень интересное задние, которое на ЕГЭ может вам встретиться под номером 18.

Условие:

Найдите все значения a, при каждом из которых система уравнений

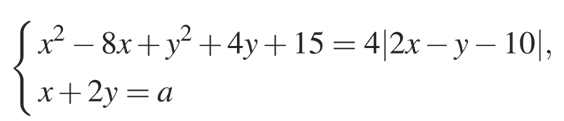
имеет более двух решений.

Решение

Эта система уравнений интересна тем, что кроме наличия параметра «а» здесь есть выражение с модулем. Конечно, это усложняет задачу, но делает её по-настоящему интересной.

Начнем решение с использования свойств выражений по модулю. Преобразуем первое уравнение системы:

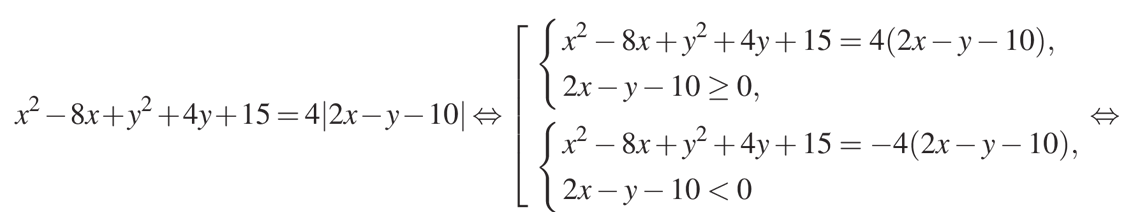
Как видите, получилось две системы, отличающиеся тем, что в первой системе мы принимаем выражение, находящееся по модулю, больше или равно нулю, а во второй системе это же выражение принимаем меньше нуля. При этом в первом уравнении второй системы нам надо учесть вводимое условие (меньше нуля) постановкой знака «-» перед правой частью.

Далее, решаем обе системы. Раскрываем скобки, переносим элементы уравнения из правой части в левую, приводим подобные члены. Вторые неравенства также преобразуем, оставляя в правой части только «у»:

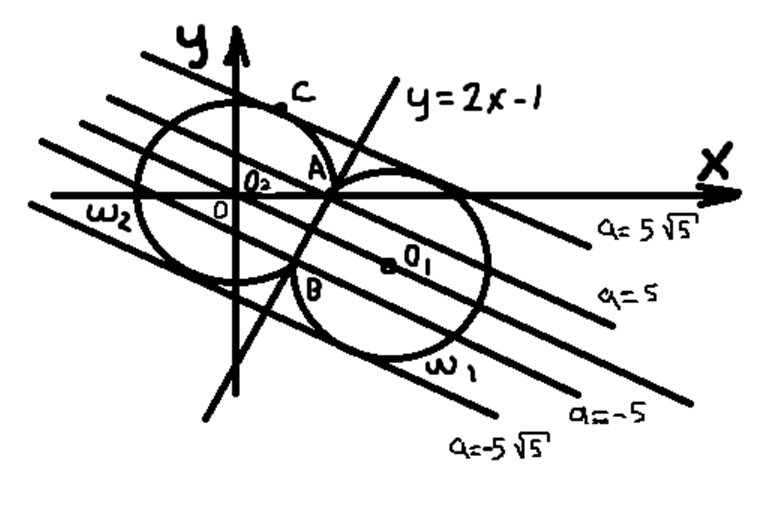
Проводим анализ получившихся выражений. Первое уравнение задаёт объединение дуг \(ω\)1 и \(ω\)2, являющихся частью окружностей радиуса 5 с центрами в точках О1(8;-4)и O2(0;0), лежащих ниже и выше прямой \(y=2x-1\) соответственно (см. рис.), пересекающихся в точках A(5;0) и B(3;-4). Заметим, что точка касания \(C( \sqrt5;2 \sqrt5)\) лежит на дуге \(ω\)2 и прямая O2C перпендикулярна прямой O1O2.

Теперь рассмотрим второе уравнение исходной системы. Оно задаёт семейство параллельных прямых, назовем их «m», которые параллельны прямой O1O2 или совпадают с ней, что зависит от величины параметра «а».

Рассмотрим несколько случаев:

При \(a=5\) , прямая «m» пересекает каждую из дуг \(ω\)1 и \(ω\)2 в точке A и ещё в одной точке, отличной от точки A, то есть исходная система при этом имеет три решения.
Аналогично, при \(a=-5\) , прямая «m» проходит через точку B и исходная система также имеет три решения.
При \(a=5\sqrt5\) , прямая «m» проходит через точку C, значит, прямая m касается дуг \(ω\)1 и \(ω\)2,то есть исходная система имеет два решения.
Аналогично, при \(a=-5\sqrt5\), прямая «m» касается дуг \(ω\)1 и \(ω\)2,то есть исходная система имеет два решения.
При \(-5\sqrt5<a<-5\) или \(5<a<5\sqrt5\), прямая «m» пересекает каждую из дуг \(ω\)1 и \(ω\)2 в двух точках, отличных от точек A и B, то есть исходная система имеет четыре решения.
При \(-5<a<5\) , прямая «m» пересекает каждую из дуг \(ω\)1 и \(ω\)2 в точке, отличной от точек A и B, то есть исходная система имеет два решения.
При \(a<-5\sqrt5\) или \(a>5\sqrt5\), прямая «m» не пересекает дуги \(ω\)1 и \(ω\)2, то есть исходная система не имеет решений.

Значит, исходная система имеет более двух решений при \(-5\sqrt5<a≤-5\) или \(5≤a<5\sqrt5\)

Для решения этой задачи мы применили как алгебраический, так и графический методы. В данном случае это дало нам наглядную картину и упростило трудоемкость при вычислениях.

Ответ: \(-5\sqrt5<a≤-5\);\(5≤a<5\sqrt5\)

Предыдущая статья