Теорема Виета

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Часто задаваемые вопросы:

19 июл 2024

Теорема Виета

Решение квадратного уравнения a·x² + b·x + c = 0. Решение: Введите коэффициенты в калькулятор уравнений по теореме Виета и нажмите "посчитать"

Давайте вспомним, что такое квадратное уравнение. Квадратное уравнение имеет вид:

Если a равно \(1\), то квадратное уравнение называется приведенным, то есть имеет вид:

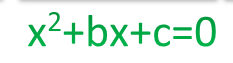
Давайте сегодня научимся решать квадратное уравнение с помощью теоремы Виета. Это возможно, если квадратное уравнение является приведенным и имеет действительные корни \(x1\) и \(x2\). Для этого надо подобрать в уме числа, удовлетворяющие условию:

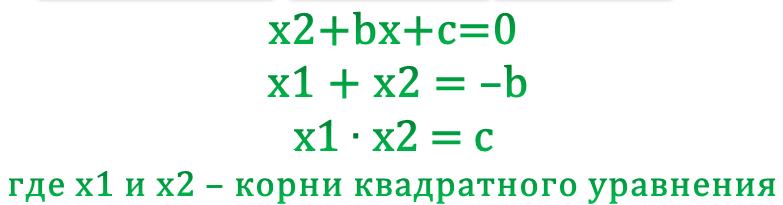
Задача 1. Решить квадратное уравнение: \(x^2-9x+14=0\)

Решение:

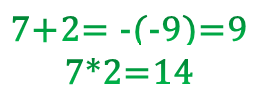
Ответ: \(7\) и \(2\).

Часто задаваемые вопросы:

✅ Какие применения имеет Теорема Виета?

↪ Теорема Виета находит широкое применение в алгебре и математике. Она позволяет быстро вычислять сумму и произведение корней уравнения, а также устанавливать связь между коэффициентами и корнями многочлена. Также она используется для факторизации многочленов и решения задач, связанных с множествами корней.

✅ Как применить Теорему Виета, если известны только суммы и произведения корней?

↪ Если известны только суммы и произведения корней, можно сформировать систему уравнений, используя формулы из Теоремы Виета, и затем решить ее, чтобы найти значения корней.

✅ Можно ли применить Теорему Виета для многочлена с комплексными корнями?

↪ Да, Теорема Виета верна не только для многочленов с действительными корнями, но также для многочленов с комплексными корнями. В этом случае важно учитывать как действительные, так и мнимые части корней при вычислениях.

Предыдущая статья