Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Эллипс
Для начала определим, что такое эллипс.
Эллипс — замкнутая кривая на плоскости, которая может быть получена как пересечение плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость. На рисунке ниже показано несколько примеров.
Круг — это частный случай эллипса, который получается, когда сечение через конус или цилиндр ортогонально оси конуса или цилиндра.

Эллипс - это фигура, в результате сечения конуса и прямого кругового цилиндра
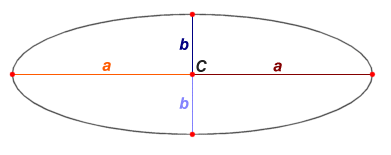
Эллипс симметричен относительно горизонтальной и вертикальной осей, как показано на рисунке выше. Максимальное расстояние между двумя точками происходит вдоль горизонтальной оси (называемой главной осью или поперечным диаметром), а минимальное расстояние между двумя точками — вдоль вертикальной оси (называемой малой осью или сопряженным диаметром). Антиподальные точки — это любые две точки по периметру эллипса, так что соединяющий их отрезок линии должен проходить через центр с эллипса (что происходит на пересечении горизонтальной и вертикальной осей). Эллипс симметричен относительно его большой и малой осей.
Полуось — это та часть оси, которая лежит между центром \(C\) и периметром эллипса. Полуоси, принадлежащие к главной оси — большая полуось, а полуось, принадлежащих к малой оси - малая полуось. На приведенной выше рисунке мы обозначили каждую из двух полуосей \(a\) и каждую из двух полуосей \(b\). Точки, показанные красным цветом по периметру эллипса, являются точками, где большая и малая оси пересекают периметр эллипса. Это вершины эллипса. Вершины - это точки, в которых кривизна эллипса максимальна (т. е. где главная ось пересекает периметр эллипса).
Как найти фокусы эллипса
Есть две специальные точки, которые лежат на главной оси эллипса, равноудаленной от его центра C, каждая из которых является фокусом эллипса.
Эти две точки (совместно называемые фокусами эллипса) обычно обозначаются как \(F1\) и \(F2\). Расположение фокусов таково, что для любой точки \(p\) по периметру эллипса сумма расстояний от \(F1\) до \(P\) и от \(F2\) до \(P\) остается постоянной и будет равна длине главной оси.
Фактически, принимая любую произвольную пару точек в качестве фокусов и любое значение длины главной оси, которое больше расстояния между этими двумя точками, соответствующий эллипс определяется как набор точек, для которых сумма расстояний между точкой и каждым из фокусов равна длине главной оси.
Сумма расстояний от фокусов до любой точки эллипса есть постоянная
Расстояние между любым из фокусов и центром эллипса называется фокусным расстоянием и будет зависеть от длины главной и малой осей. Мы обозначили отрезки линии, соединяющие каждый фокус с центром эллипса \(C\). Длину\( c\) (т. е. Фокусное расстояние) можно найти по следующей формуле:
\(с= \sqrt{a^2-b^2} \)
где \(a\) и \(b\) - длины главной и малой осей соответственно. Обратите внимание, что чем дальше фокусы от центра эллипса, тем меньше сходство между эллипсом и окружностью. Кривизна в вершинах эллипса будет увеличиваться, в то время как кривизна в \(cо\) - вершинах будет уменьшаться. Другими словами, эллипс станет более плоским по мере увеличения значения \(c\).

Уравнение эллипса (рис.1) :
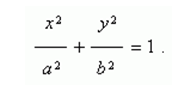
Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ ( рис.1 ) , при a < b фокусы эллипса лежат на оси ОY , а при a = b эллипс становится окружностью (фокусы эллипса в этом случае совпадают с центром окружности ). Таким образом, окружность есть частный случай эллипса.
Отрезок F1F2 = 2 с ,
где ![]()

называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осью эллипса. Число e = c / a , e< 1 называется эксцентриситетом эллипса.
Пусть Р ( х1 , у 1 ) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид:
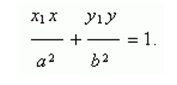
Условие касания прямой y = m x + k и эллипса х 2 / a 2 + у 2 / b 2 = 1 :
k 2 = m 2 a 2 + b 2 .
Часто задаваемые вопросы
Как связаны полуоси эллипса с его геометрической структурой?
Большая полуось "a" определяет ширину эллипса, а малая полуось "b" - его высоту. Соотношение a и b определяет степень "приплюснутости" или "растянутости" эллипса.
Какую роль играет фокусное расстояние в эллипсе?
Фокусное расстояние "f" определяет расстояние от центра эллипса до каждого из его фокусов и связано с полуосью через формулу: \(f = √(a^2 - b^2)\).
Каковы основные характеристики эллипса?
Основные характеристики эллипса - большая и малая полуоси, фокусы, эксцентриситет и фокусное расстояние.
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Подготовка к ЕГЭ по математике профильный уровень
Подготовка к ЕГЭ по математике профильный уровень -
 Репетитор для подготовки к ОГЭ по химии
Репетитор для подготовки к ОГЭ по химии -
 Репетитор для подготовки к ЕГЭ по физике
Репетитор для подготовки к ЕГЭ по физике -
 Репетитор по английскому ОГЭ
Репетитор по английскому ОГЭ -
 Репетитор по английскому с нуля
Репетитор по английскому с нуля -
 Репетитор по английскому для взрослых
Репетитор по английскому для взрослых -
 Подготовка к ВПР по русскому
Подготовка к ВПР по русскому -
 Подготовка к ОГЭ по биологии
Подготовка к ОГЭ по биологии -
 Репетитор для подготовки к ЕГЭ по географии
Репетитор для подготовки к ЕГЭ по географии -
 Подготовка к ЕГЭ по информатике
Подготовка к ЕГЭ по информатике


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

