Площади трапеции

Дарим в подарок бесплатный вводный урок!

Предметы

Специализации

Чему равна площадь трапеции?

Чтобы вычислить площадь трапеции, необходимо знать длины ее двух параллельных сторон (оснований) и высоту, которая перпендикулярна к основаниям.

Складываем основания трапеции, делим сумму на два и умножаем все это на высоту, проведенную к большему основанию.

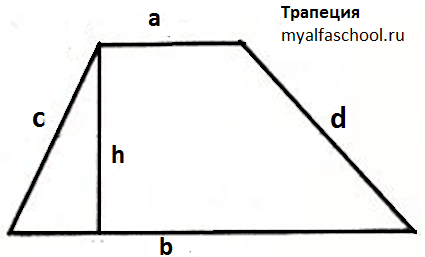
\(S=\frac{a+b}{2}h\)

Первое основание трапеции a:

Второе основание трапеции b:

Высота трапеции:

Как найти площадь трапеции: формула Герона

Также мы можем вычислить площадь трапеции зная все стороны трапеции (формула Герона):

\(s=\frac{a+b}{|a-b|}\sqrt{(p-a)(p-b)(p-a-c)(p-a-d)}\)

где: \(p=\frac{a+b+c+d}{2}\)

Первая сторона трапеции a:

Вторая сторона трапеции b:

Третья сторона трапеции c:

Четвертая сторона трапеции d:

Как найти площадь трапеции через диагонали и высоту

Если известны длины всех четырех сторон трапеции, можно воспользоваться формулой:

\(S = ((a + b) / 2) * sqrt(c^2 - ((b - a)^2 + h^2) / 4)\)

, где a и b - длины оснований, c - длина диагонали трапеции, а h - высота, опущенная на основание.

Как найти площадь трапеции через диагонали и угол между ними

Чтобы найти площадь трапеции через диагонали и угол между ними, необходимо знать длины диагоналей d1 и d2, и угол между ними. После этого можно воспользоваться формулой:

\(S = (d1 * d2 * sin(θ)) / 2\)

, где θ - угол между диагоналями (измеряется в радианах).

Для того, чтобы использовать эту формулу, угол между диагоналями должен быть измерен в радианах. Если угол задан в градусах, его необходимо перевести в радианы, умножив на π/180.

Часто задаваемые вопросы

✅ Что такое трапеция?

↪ Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие - нет. Стороны, которые параллельны, называются основаниями трапеции, а высотой трапеции называется отрезок, соединяющий основания и перпендикулярный им обеим.

Форма трапеции напоминает букву "T". Трапеции встречаются в геометрии очень часто, и они имеют множество свойств и формул для вычисления различных параметров.

✅ Какие основные свойства трапеции?

↪ Основные свойства трапеции: Две стороны параллельны, а две другие - нет. Углы, лежащие на одной основании, дополнительны. Сумма углов трапеции равна 360 градусам. Высота трапеции является перпендикуляром, опущенным на основания.

Сумма длин боковых сторон трапеции всегда больше длины ее оснований. Диагонали трапеции делят ее на четыре подобные треугольника.

Больше уроков и заданий по всем школьным предметам в онлайн-школе "Альфа". Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Зоя Юрьевна Духненко

Репетитор по математике

Стаж (лет)

Образование:

Душанбинский государственный педагогический институт им. Т. Г. Шевченко

Проведенных занятий:

1059

Форма обучения:

Дистанционно (Скайп)

Михаил Николаевич Макеев

Репетитор по математике

Стаж (лет)

Образование:

Московский энергетический институт

Проведенных занятий:

755

Форма обучения:

Дистанционно (Скайп)

Татьяна Валентиновна Дмитриева

Репетитор по математике

Стаж (лет)

Образование:

Ивановский государственный университет

Проведенных занятий:

1174

Форма обучения:

Дистанционно (Скайп)