О платформе 
Премиум математика 
Репетиторы 
Тарифы 
Вход
Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок
Накрест лежащие углы
#Математика
#Подготовка к ЕГЭ
#ЕГЭ по математике
#ОГЭ по математике
#Подготовка к ОГЭ
Обновлено: 06 авг 2024
Накрест лежащие углы
Когда секущая пересекает пару параллельных линий, образуются накрест лежащие углы. Накрест лежащие углы равны друг другу.
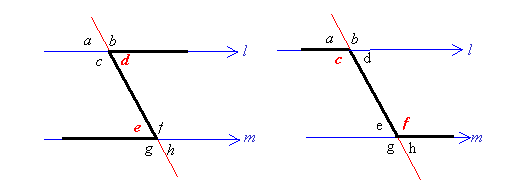
Один из способов найти накрест лежащие углы - нарисовать зигзагообразную линию на рисунке, \(d\) и \(e\) , \(c\) и \(f\) являются накрест лежащими углами.
Пример 1: На приведенной ниже рисунке определите значения углов \(b, c, d, e, f, g , h\).
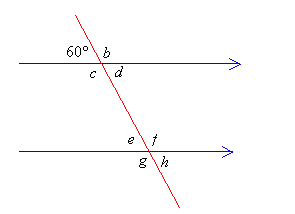
Решение:
- \(b + 60° =180° ⇒ b = 180° – 60° = 120°\)
- \(b\) и \(c\) - вертикальные углы. Поэтому \(c = b = 120°\)
- \(d\) и \(60°\) вертикальные углы. Поэтому \(d = 60°\)
- \(e = d = 60°\)
- \(f+ 60° =180° ⇒ f = 180° – 60° = 120°\)
- \(g\) и \(f-\)вертикальные углы. \(g = f = 120°\)
- \(h\) и \(e-\)вертикальные углы. Поэтому \(h = e = 60°\)
Ответ: \(b = 120°, c = 120°, d = 60°, e = 60°, f = 120°, g = 120° , h = 60°\)
Дарим в подарок бесплатный вводный урок!
Репетиторы
Похожие статьи
Округление десятичных дробей
Обновлено: 14 авг 2024
Сложение и вычитание отрицательных дробей
Обновлено: 14 окт 2024
Движение навстречу друг другу
Обновлено: 20 июн 2024
Решаем ОГЭ по математике. Задание №5. 2
Обновлено: 21 мар 2025
Преобразование алгебраических выражений
Обновлено: 18 июл 2024
Решаем ОГЭ. Задание 21
Обновлено: 07 май 2024
Решаем профильный ЕГЭ. №17. Оптимизация
Обновлено: 24 дек 2024
ЕГЭ по математике, базовый уровень. Задачи на движение по прямой (вариант 1)
Обновлено: 10 май 2024