Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Призма
Призма представляет собой многогранник - трехмерную геометрическую фигура с плоскими гранями и прямыми ребрами, которые имеет одинаковую форму поперечного сечения по всей длине и ограниченной на каждом конце двумя равными и параллельными многоугольниками. Остальные грани призмы (боковые грани) являются параллелограммами. Треугольная призма показана ниже:

Если количество сторон одного из могоугольников в основании призмы равно \(n\), то призма будет иметь \(N + 2\) грани, \(3n\) ребер и \(2n\) вершин.
Треугольная призма
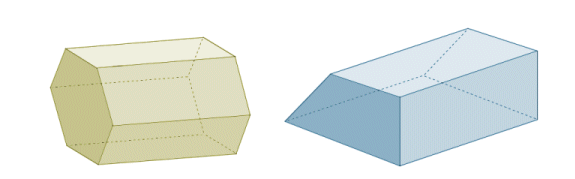
Также вы можете встретить правильную призма, то есть все базовые грани в основании призмы являются правильными многоугольниками. Из этого следует, что все боковые грани неправильной призмы не будут иметь одинаковые размеры.
Регулярная шестиугольная призма (слева) и неправильная призма (справа)
Возникает интересный вопрос о том, можно ли иметь цилиндрическую призму. Если боковые грани цилиндра оба равны и параллельны, то сечение, безусловно, соответствуют требованиям призмы. Точка прилипания находится над требованием, что базовые грани призмы должны быть многоугольниками. Поскольку базовая грань цилиндра должна быть либо кругом, либо эллипсом, часто утверждается, что цилиндр не может быть призмой, потому что ни круг, ни эллипс не являются многоугольником. С другой стороны, можно также утверждать, что, поскольку теоретически нет предела количеству сторон, которые может иметь многоугольник, круг (или эллипс) - это просто многоугольник с бесконечным числом сторон.
Как найти объем призмы. Для правильной призмы найти объем относительно просто. Все, что нам нужно сделать, это умножить площадь одной базовой грани призмы на длину призмы. Здесь полезно думать о призме как о стоящей на одной из ее базовых граней. Длина призмы это высота \(h\). Поэтому мы можем написать формулу для нахождения объема \(V\) призмы как:
\(V = S_{осн}h\)
Это также работает для косой, смещенной призмы, если мы рассматриваем высоту как перпендикулярное расстояние между двумя базовыми гранями.
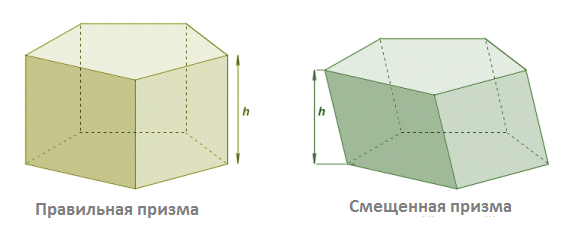
Высота призмы - это перпендикулярное расстояние между ее гранями в основании.
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор по олимпиадной математике
Репетитор по олимпиадной математике -
 Репетитор по алгебре
Репетитор по алгебре -
 Репетитор для подготовки к ЕГЭ по химии
Репетитор для подготовки к ЕГЭ по химии -
 Подготовка к сочинению по русскому языку
Подготовка к сочинению по русскому языку -
 Подготовка к ЕГЭ по английскому онлайн
Подготовка к ЕГЭ по английскому онлайн -
 Подготовка к ОГЭ по английскому языку
Подготовка к ОГЭ по английскому языку -
 Репетитор по английскому с нуля
Репетитор по английскому с нуля -
 Репетитор по истории ОГЭ
Репетитор по истории ОГЭ -
 Репетитор по обществознанию ВПР
Репетитор по обществознанию ВПР -
 Репетитор для подготовки к ЕГЭ по географии
Репетитор для подготовки к ЕГЭ по географии


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

