Трапеция, средняя линия трапеции
- Подготовка к ЕГЭ по математике (профильный уровень)
- Подготовка к олимпиадам по физике
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Репетитор по английскому языку для подготовки к ЕГЭ
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор для подготовки к ЕГЭ по обществознанию
- Репетитор для подготовки к ОГЭ по обществознанию
- Репетитор по географии для подготовки к ЕГЭ
- Подготовка к ОГЭ по литературе
- Программирование Pascal
Как называются стороны трапеции
- \(DE\) и \(CF\) называются высотами трапеции.
- \(AD\) и \(BC\) боковые стороны трапеции.
- \(AB\) и \(CD\) основания трапеции.
Как найти среднюю линию трапеции
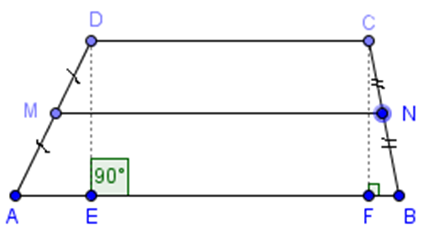
- \(MN\) - средняя линия трапеции \(ABCD\). \(M\) - середина \(AB\), \(N\)- середина \(BC\).
- \(AM\) \(= MD\); \(BN = NC;\)
Как найти боковые стороны трапеции
Для нахождения боковых сторон трапеции необходимо знать длины оснований и длину средней линии (медианы) трапеции.
Если известны длины оснований трапеции (a и b) и длина средней линии (m), то боковые стороны трапеции могут быть найдены с использованием следующих формул:
Боковая сторона a = m - b
Боковая сторона b = m - a
Таким образом, чтобы найти длины боковых сторон трапеции, вычитайте длину каждого основания из длины средней линии.
Важно помнить, что эти формулы работают только при условии, что известны длины оснований и длина средней линии трапеции. Если у вас есть другие известные значения, такие как углы или высота трапеции, то можно использовать дополнительные геометрические свойства и теоремы для нахождения боковых сторон.
Теорема 2.
\(MN=\frac{AB + DC}{2}\)
Часто задаваемые вопросы:
✅ Что такое основания трапеции?
↪ Основания трапеции - это две параллельные стороны трапеции, которые находятся на противоположных концах фигуры. Одно основание обычно длиннее другого.
✅ Как называются непараллельные стороны трапеции?
↪ Непараллельные стороны трапеции называются боковыми сторонами или наклонными сторонами. Они соединяют соответствующие концы оснований и не равны друг другу.
✅ Что представляет собой средняя линия (медиана) трапеции?
↪ Средняя линия (медиана) трапеции - это отрезок, соединяющий середины боковых сторон. Она параллельна основаниям и делит трапецию на две равные по площади части.
