Модуль числа (Часть 2)
Модуль абсолютная величина числа
КВАДРАТНЫЕ КОРНИ
Продолжение статьи Модуль числа (Часть 1)
\( (3)^2 = 9\)
\(b = 3\)
но!!!
\( (-3)^2 = 9 \) \(b = -3\)
\(b = 3\)
но!!!
\( (-3)^2 = 9 \) \(b = -3\)
Положительный квадратный корень квадрата числа равен этому числу.
Теорема
Для любого действительного числа \(a\)
\(\sqrt{a^2} = |a|\)
\( \sqrt{(-4)^2} = \sqrt{16} = 4 = |-4|\)
Для любого действительного числа \(a\)
\(\sqrt{a^2} = |a|\)
\( \sqrt{(-4)^2} = \sqrt{16} = 4 = |-4|\)
\(|- a| = | a |\) a имеет одинаковые абсолютные значения.
\(| ab | = |a|*|b|\) произведение модуля является произведением абсолютных значений.
\(|\frac{ a} {b}| =\frac{ |a|} { |b|}\) -деление модуля равно отношению абсолютных значений.
Доказательство
\(| ab | = |a|*|b|\) произведение модуля является произведением абсолютных значений.
\(|\frac{ a} {b}| =\frac{ |a|} { |b|}\) -деление модуля равно отношению абсолютных значений.
Доказательство
\( 1) |-a| = \sqrt{(- a) ^2} = \sqrt{a^2} = |a|\)
\(2) |ab| = \sqrt{(ab)^2} =\sqrt{a^2b^2} = \sqrt{a^2}\sqrt{b^2} = |a||b|\)
\( |-4| = |4| \)
\( |2*(-3)| = |-6| = 6 = |2|*|3| = 6\)
\( |5/4| = 5/4 = |5|/|4| = 5/4\)
Геометрическая интерпретация абсолютной величины
Геометрическая интерпретация абсолютной величины
Где A и B-точки с координатами a и b. Расстояние между A и B
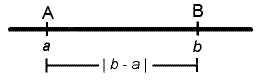
Если \(a\) и \(b\) являются точками на координатной линии с координатами A и b соответственно, то расстояние \( d\) между A и B
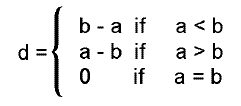
\( d = |b-a| \)
\(| x-a | < k (k>0)\)
\(| x-a | < k (k>0)\)
Другая форма записи
-\(k < x-a < k \)
Пример 1. Решить неравенство
\( | x-3 |< 4 \)
записываем как:
\( -4 < х-3 < 4 \)
прибавляем \(3\) с обоих сторон:
\( -1 < x < 7 \)
Ответ: \( (-1,7)\)
Пример 1. Решить неравенство
\( | x-3 |< 4 \)
записываем как:
\( -4 < х-3 < 4 \)
прибавляем \(3\) с обоих сторон:
\( -1 < x < 7 \)
Ответ: \( (-1,7)\)
Пример 2. Решить неравенство:
Решить \( |x+4 |≥ 2 \)
\( x+4 ≤ -2\)
\(х ≤ -6 х+4 ≥ 2\)
\(x≥ -2\)
Ответ: объединение из двух промежутков:
\( (-∞ , -6] ∪ [-2 , +∞ )\)
Решить \( |x+4 |≥ 2 \)
\( x+4 ≤ -2\)
\(х ≤ -6 х+4 ≥ 2\)
\(x≥ -2\)
Ответ: объединение из двух промежутков:
\( (-∞ , -6] ∪ [-2 , +∞ )\)
Наши преподаватели
Репетитор по математике
Стаж (лет)
16
Образование:
Гомельский государственный университет им. Ф. Скорины
Проведенных занятий:
265
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
4
Образование:
Южно-Уральский Государственный Гуманитарно Педагогичесий Университет
Проведенных занятий:
56
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
18
Образование:
Южный федеральный университет
Проведенных занятий:
634
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по олимпиадной математике
- Подготовка к ЕГЭ по английскому языку
- Разговорный английский язык
- Репетитор для подготовки к ЕГЭ по истории
- Репетитор по истории для подготовки к ОГЭ
- Репетитор для подготовки к ВПР по русскому языку
- ВПР по обществознанию
- Репетитор для подготовки к ЕГЭ по обществознанию
- Подготовка к ЕГЭ по информатике
Похожие статьи
- Производная
- Формула площади эллипса
- Значение синуса, косинуса и тангенса 30°, 45° и 60°
- Распределительное свойство умножения
- РУДН: факультет ветеринарии
- ЕГЭ по математике, базовый уровень. Задачи с показательными уравнениями и неравенствами
- Советы родителям и учителям по организации учебы гиперактивных детей
- Как приготовить овощи, каши и мясо, чтобы ребенок их съел
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так