Средняя линия треугольника

Дарим в подарок бесплатный вводный урок!

Предметы

Специализации

Определение

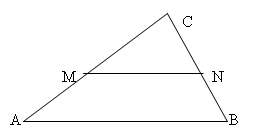
$AM = MC ; BN = NC =>$
$MN || AB$
$MN = \frac{AB }{ 2}$

Теорема о средней линии треугольника

Теорема о средней линии треугольника - это геометрическое утверждение, связанное со средними линиями треугольника и их свойствами.

Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Другими словами, в треугольнике со сторонами $a$ , $b$ и $c$ , средняя линия, проведенная из середины стороны $a$ , будет параллельна $a$ и равна половине длины стороны $a$ . Аналогично для средних линий, проведенных из середин других сторон.

Эта теорема имеет важное геометрическое значение, и она также используется в решении различных задач, связанных с треугольниками.

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:

$MN\parallel AC;$

$MN = \frac{1}{2}AC$

Свойства средней линии треугольника

Средняя линия треугольника - это отрезок, соединяющий середины двух сторон треугольника. У средних линий есть несколько интересных свойств:

Параллельность: каждая средняя линия параллельна соответствующей стороне треугольника. То есть, если $A B$ и $C D$ - стороны треугольника, а $E$ и $F$ - середины этих сторон, то средняя линия $EF$ параллельна $A B$ и $C D$ .
Деление в отношении 2:1: центр масс треугольника (точка пересечения средних линий) делит каждую среднюю линию в отношении 2:1. Это означает, что более короткие отрезки, образованные центром масс и каждой из вершин треугольника, равны половине длины более длинного отрезка.
Равенство площадей четырехугольников: если провести средние линии из вершин треугольника, то они образуют шесть маленьких треугольников и три четырехугольника. Площади этих четырехугольников равны между собой.
Сравнение длин: длина средней линии меньше длины самой длинной стороны треугольника, но больше длины самой короткой стороны.

Эти свойства делают средние линии треугольника полезными инструментами в геометрических рассуждениях и задачах.

Деление отрезка на равные части

Разделим данный отрезок $AB$ на $5$ равных частей.
Пусть $p$-произвольный луч с началом $A$ и $p$ не лежит на $АВ$. Нарисуем пять последовательно равных треугольников.

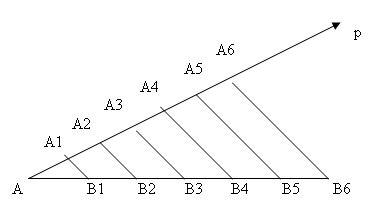
$АА_1 = А_1А_2 = A_2A_3 = A_3A_4 = A_4A_5$

Соединим $A_5$ с $B$ и нарисуем линии через $A_4, A_3, A_2$ и $A_1$, которые параллельны $A_5B$. Они пересекают $AB$ соответственно в точках $B_4, B_3, B_2$ и $B_1$. Эти точки делят отрезок $AB$ на пять равных частей.

$А_1B_1 ||А_2B_2 ||A_2B_2 || A_3B_3 ||A_4B_4 ||A_5B_5 ||A_6B_6$

И $AB_1 = B_1B_2 = B_2B_3 = B_3B_4 = B_4B_5=B_5B_6$

Понятно, что если $AB$ разделить на другое количество равных частей, у нас получится то же самое.

Часто задаваемые вопросы:

✅ Зачем нужны средние линии треугольника?

↪ Средние линии треугольника обладают рядом интересных свойств. Одно из них - центр масс треугольника (точка пересечения средних линий) делит каждую среднюю линию в отношении 2:1, где две более короткие части равны одной более длинной.

✅ Как найти точку пересечения средних линий?

↪ Центр масс треугольника (точка пересечения средних линий) может быть найден как среднее арифметическое координат вершин треугольника.

✅ Может ли треугольник иметь среднюю линию, длина которой равна нулю?

↪ Да, треугольник может иметь среднюю линию длиной ноль, если он вырожденный, то есть все его вершины лежат на одной прямой.

Больше уроков и заданий по всем школьным предметам в онлайн-школе "Альфа". Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Денис Валерьевич Кочнев

Репетитор по математике

Стаж (лет)

Образование:

Омский государственный педагогический университет

Проведенных занятий:

425

Форма обучения:

Дистанционно (Скайп)

Светлана Валентиновна Емец

Репетитор по математике

Стаж (лет)

Образование:

Государственное образовательное учреждение высшего профессионального образования "Самарский государственный педагогический университет"

Проведенных занятий:

316

Форма обучения:

Дистанционно (Скайп)

Маргарита Руслановна Мередова

Репетитор по математике

Стаж (лет)

Образование:

УРСПК

Проведенных занятий:

1077

Форма обучения:

Дистанционно (Скайп)