Центральный угол окружности

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Как найти центральный угол окружности

Для начала разберем, что такое центральный угол окружности.

Центральный угол окружности образуется двумя радиусами. Окружность состоит из дуг и центральных углов. Центральный угол измеряется с помощью длины дуги и радиуса. Задачи центрального угла могут быть решены с помощью формулы центрального угла.

На рисунке ниже центральный угол окружности, угол \(θ\), образованный между двумя радиусами:

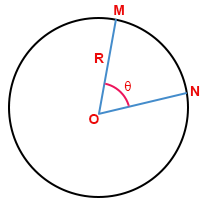
Центральный угол равен градусной мере дуги, на которую он опирается.

\(∠ MON =MN\)

Как найти центральный угол окружности

Чтобы понять, чему равен центральный угол окружности, используют формулу. Формула для центрального угла в градусах окружности вычисляется следующим образом, если известна длина дуги в метрах, сантиметрах и др.

\( a=\frac{L*360}{2*π×r}\)

\(L-\)длина дуги

Пример 1. Найдите Центральный угол, если длина радиуса \(11\) см, а длина дуги около \(14\) см?

Решение:

Найдем Центральный угол окружности по формуле:

\(θ =\frac{ 14 × 360}{2 × 3.14 × 11}=\frac{5040}{69,08}=72,95\)

Центральный угол равен \(72,95\) градуса

Часто задаваемые вопросы

Что такое центральный угол окружности?

Центральный угол окружности - это угол, вершина которого находится в центре окружности, а стороны проходят через две точки на окружности.

Каковы основные свойства центрального угла окружности?

Основные свойства центрального угла окружности: 1) Его величина равна мере дуги, на которую он опирается. 2) Центральный угол, опирающийся на полную окружность, равен 360 градусов (или 2π радиан). 3) Апотема (перпендикуляр от центра к хорде) делит центральный угол на два равных угла.

Как использовать центральные углы окружности в задачах и конструкциях?

Центральные углы окружности широко используются в задачах и конструкциях, связанных с геометрией и тригонометрией. Они помогают определять меры дуг, длины хорд, а также решать задачи на нахождение неизвестных углов и длин отрезков внутри окружности. Также, центральные углы могут использоваться для построения различных геометрических фигур и конструкций.

Предыдущая статья

Следующая статья

Как найти центральный угол окружности

Дарим в подарок бесплатный вводный урок!

Центральный угол окружности

Как найти центральный угол окружности

Часто задаваемые вопросы

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи