10 фактов о треугольнике

 

Треугольник рассматривается как фундаментальная форма геометрии, которая может быть многоугольником, состоящим из трех углов и трех сторон, которые являются отрезками линии. Треугольники классифицируются на основе двух критериев, которые задаются относительной длиной их сторон и их внутренними углами. Существуют различные типы треугольников. В этой статье Альфа-школа расскажет вам \(10\) фактов о треугольниках.

 

Факт 1: В треугольнике внешний угол рассматривается как линейная пара к внутреннему углу, а сумма трех внешних углов любых треугольников равна \(360°\) градусам.

---

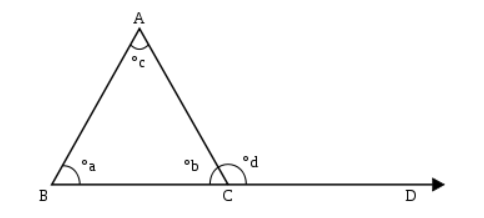
Факт 2: внешний угол любого треугольника будет равен сумме двух внутренних углов этого треугольника, которые не примыкают к этому внешнему углу.

---

Факт 3: Неравенство треугольника треугольника утверждает, что сумма длин любых двух сторон треугольника всегда будет больше, чем длина третьей стороны этого треугольника.

---

 

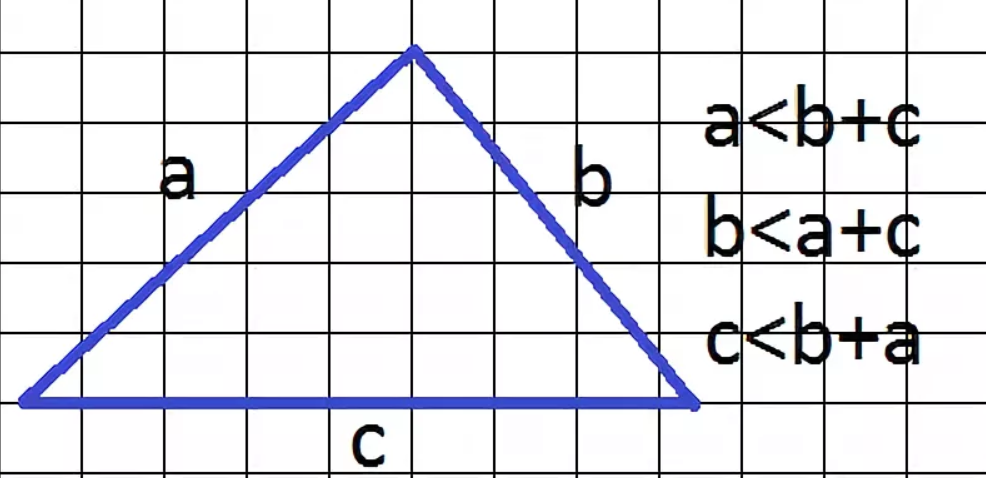
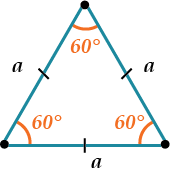
Факт 4: в треугольнике, если все стороны считаются равными, то он называется равносторонним треугольником. Он также называется правильным многоугольником с  углами \(60°\).  \(S\) равностороннего треугольника:

 

---

Факт 5: если только две стороны у треугольника  равны, то мы называем его равнобедренным треугольником.

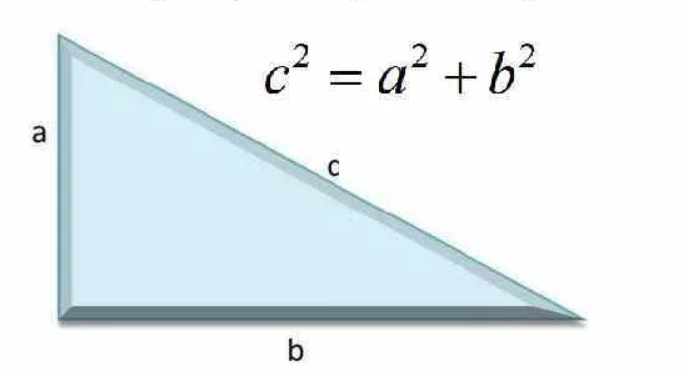
Факт 6: прямоугольный треугольником называется треугольником, если сумма квадратов смежных стороны равна квадрату гипотенузы,  \(c-\)гипотенуза.

---

 

Факт 7: радиус описанной окружности равностороннего треугольника \(R\) :

 

\(\frac{a√3}{3}\)  или \(\frac{a}{√3}\)

---

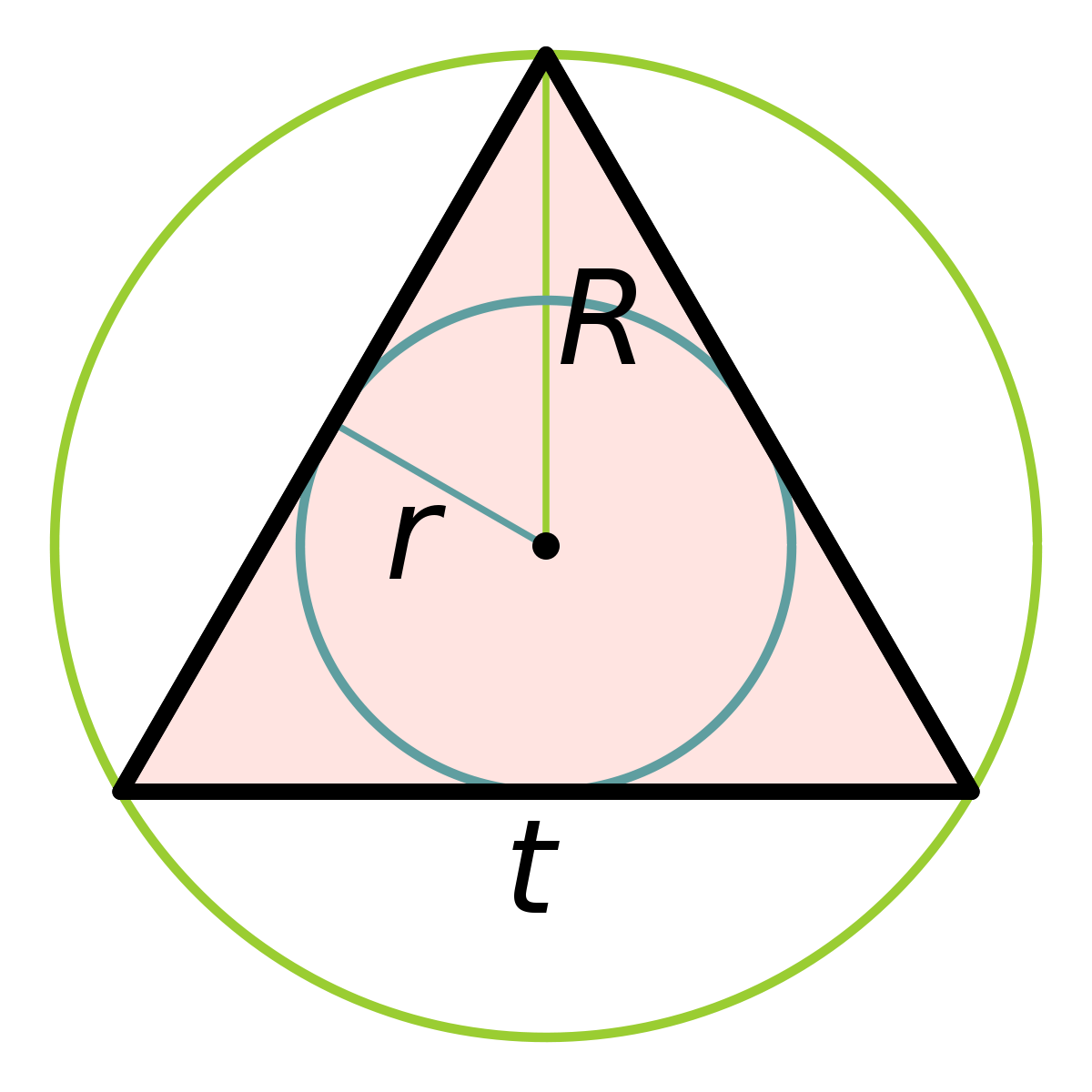
Факт 8:   радиус вписанной окружности  равностороннего треугольника \(r\)  :

---

 

Факт 9: когда треугольник имеет один из своих углов, измеряющих более \(90°\) градусов, треугольник называется тупым треугольником.

---

Факт 10: внутренние углы треугольника всегда равны \(180°\) градусам.