Конус

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Часто задаваемые вопросы:

23 июн 2024

Конус

Конус — это трехмерный объект, несколько похожий по форме на пирамиду. На самом деле, вы можете представить себе конус как пирамиду, которая имеет бесконечное количество сторон (или, другими словами, пирамиду с круглым основанием).

Однако конус не является многогранником, просто потому, что он имеет круглое основание. То есть основание конуса — это окружность. Она имеет одну вершину (вершину конуса), которая лежит на некотором расстоянии от основания и в другой плоскости. В то время как пирамида имеет конечное число треугольных сторон, каждая из которых соединяет одну сторону базового многоугольника с вершиной пирамиды, конус имеет единую, плавно изогнутую и коническую боковую поверхность, которая соединяет круглое основание конуса с его вершиной.

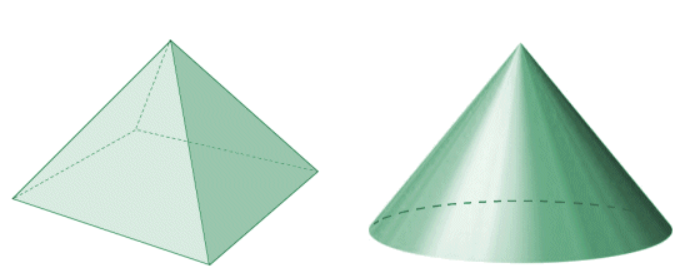
На рисунке ниже показана квадратная пирамида и типичный конус с аналогичными пропорциями.

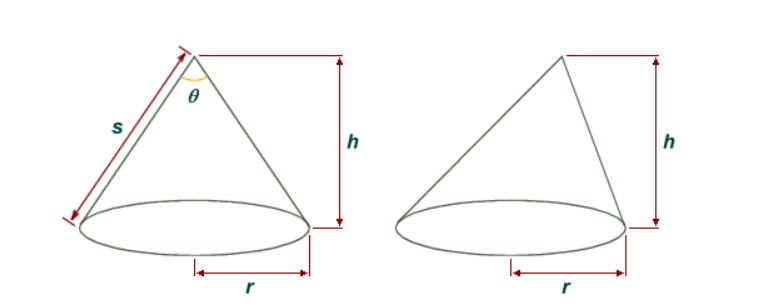
На рисунке ниже, для прямого кругового конуса и наклонного кругового конуса, \(r\) - радиус основания, а \(h\)- высота конуса. На рисунке конуса слева \(s\) - наклонная высота конуса, то есть расстояние между вершиной конуса и периметром основания конуса.

փ-апертура конуса - это максимальный угол, который может существовать между двумя отрезками линии, соединяющими основание конуса с его вершиной.

Конус: формулы

Формула для нахождения объема кругового конуса (правого или смещенного) в значительной степени совпадает с формулой для нахождения объема пирамиды. Объем \(V\) будет произведением площади основания конуса \(S_{осн}\) и вертикальной высоты конуса \(h\), умноженной на одну треть. Мы можем выразить это формально как:

\(V =\frac{ 1}{3} S_{осн}h\)

Обратите внимание, что это та же формула, которая используется для поиска объема пирамиды. Однако, поскольку основание конуса является окружностью, а площадь окружности вычисляется как \(\pi r^2\), где \(r\) - радиус окружности, то если мы подставим в формулу выше площадь окружности получим формулу объема конуса:

\(V =\frac{ 1}{3} \pi r^2 h\)

Часто задаваемые вопросы:

✅ Что такое конус?

↪ Конус - это геометрическое тело, которое имеет круглую основу и сужающуюся к вершине форму. Основа конуса может быть любой формы, но чаще всего это круг. Он отличается от цилиндра тем, что его боковая поверхность сужается к одной точке - вершине конуса.

✅ Каковы основные элементы конуса?

↪ Конус состоит из нескольких основных элементов. Основа конуса - это круг, который находится в его нижней части. Высота конуса - это расстояние между основой и вершиной. Радиус основы - это расстояние от центра основы до ее края. Апофема - это линия, соединяющая вершину конуса с центром основы.

✅ Как вычислить объем и площадь поверхности конуса?

↪ Объем конуса можно вычислить по формуле \(V = (1/3) * π * r^2 * h\), где r - радиус основы, h - высота конуса. Площадь поверхности конуса вычисляется по формуле S = π * r * (r + l), где r - радиус основы, l - апофема (расстояние от вершины до края основы).

Предыдущая статья