С 10 до 22.00 по МСК ежедневно
Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок
Свойства прямоугольного треугольника
23 май 2024
Свойства прямоугольного треугольника
Прямоугольный треугольник
Треугольник с прямым углом \(90°\) называют прямоугольным треугольником.
Самая длинная сторона треугольника называется гипотенузой, а две другие стороны - катеты.
Свойства прямоугольного треугольника - это свойства, определяющие прямоугольный треугольник.
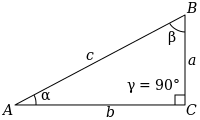
- Если угол \(α\) равен \(30°\) градусов, то \(2a = c\).
- Площадь прямоугольного треугольника можно измерить с помощью формулы:
\(S = \frac{1}{2}×a×b\),
где \(a\) и \(b\) можно рассматривать как две стороны треугольника. Эта формула используется только для прямоугольного треугольника.
- Теорема Пифагора утверждает, что если \(c\)- гипотенуза, а \(a\) и \(b\) - две стороны треугольника, то в соответствии с теоремой Пифагора:
\( c^2=a^2+b^2\)
Квадрат гипотенузы равен сумме квадрата двух других сторон треугольника.
- Радиус вписанной окружности прямоугольного треугольника можно найти по формуле:
\(r = \frac{a+b-c}{2}\)
- Радиус описанной окружности прямоугольного треугольника можно рассчитать по формуле:
\(r=\frac{c}{2}\),
где \(c\) - гипотенуза прямоугольного треугольника.
- Проекции катетов треугольника на гипотенузу:
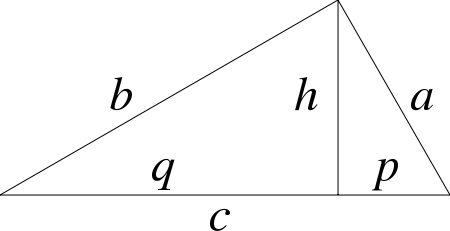
\(b^2=q*c\)
\(a^2=p*c\)
\(h^2=q*p\)
Дарим в подарок бесплатный вводный урок!
Репетиторы
![arrow]()
Специализация
![arrow]()
-
![rhombus]()
Подготовка к ЕГЭ по математике (базовый уровень) -
![rhombus]()
Репетитор по алгебре -
![rhombus]()
Репетитор для подготовки к ОГЭ по физике -
![rhombus]()
Репетитор по русскому языку для подготовки к ОГЭ -
![rhombus]()
Репетитор по английскому языку для подготовки к ОГЭ -
![rhombus]()
Репетитор для подготовки к ЕГЭ по обществознанию -
![rhombus]()
Репетитор по географии для подготовки к ЕГЭ -
![rhombus]()
Подготовка к ОГЭ по литературе -
![rhombus]()
Программирование Pascal -
![rhombus]()
Scratch
Похожие статьи
Признаки делимости (Часть 1)
23 май 2024
Производная
23 июл 2024
Задачи на проценты
23 июл 2024
Площадь параллелепипеда
23 авг 2024
Сколько одно число составляет в процентах от другого?
23 авг 2024
Что делать, если родители против выбранной профессии?
23 июл 2024
Один дома: чем заняться без родителей и как избежать проблем
23 ноя 2024
Почему не стоит пользоваться маминой косметикой
23 янв 2024