Ромб

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Обновлено: 22 мар 2024

Ромб

Ромб-это равносторонний четырехугольник то есть у него есть четыре стороны, которые равны по длине, но углы могут быть не равны. Противоположные стороны ромба перпендикулярны биссектрисам ромба, и разрезают друг друга ровно пополам под прямым углом. Ромб является частным случаем параллелограмма в том, что все четыре стороны равны по длине, а не только противоположные стороны. Квадрат-это частный случай ромба, в котором все углы равны \(90°\). Ромб-это причудливое научное название "алмаза". Это одно и то же. Простыми словами -это наклонный квадрат.

Ромб

Основные свойства ромба

Ромб

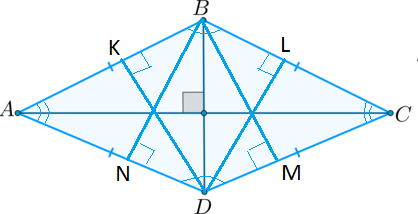
Как вычислить площади ромба ты найдешь в этой статье: https://myalfaschool.ru/articles/ploshhadi-romba.

Обладает всеми свойствами параллелограмма
Диагонали перпендикулярны:

\( AC ⊥ BD\)

Диагонали биссектрисы угла:

\(∠BAC = ∠CAD, ∠ABD = ∠DBC; ∠BCA = ∠ACD, ∠ADB = ∠BDC\)

Сумма квадратов диагоналей равна сумме квадратов сторон:

\(AC^2 + BD^2 = 4AB^2\)

Точка пересечения диагоналей является центром симметрии.
В любой ромб можно вписать окружность.
Центром окружности является точка пересечения диагоналей.

Сторона ромба

Сторона ромба формулы:

Формула стороны ромба через площадь и высота:

\(a=\frac{c}{h_a}\)

Формула стороны ромба через площадь и радиус вписанной окружности:

\(a=\frac{S}{2r}\)

Формула стороны ромба через его диагонали:

\(а =\frac{ \sqrt{d_1^2 + d_2^2}}2\)

Формула стороны ромба через периметр:

\(a=\frac{P}{4}\)

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

line

gift

Репетиторы

Специализация

Похожие статьи

Скалярное произведение векторов

Обновлено: 11 фев 2024

Свойства скалярного произведения

Обновлено: 10 дек 2023

Как найти делимое?

Обновлено: 16 мар 2024

Как построить график гиперболы?

Обновлено: 05 май 2024

Решаем задание №17. Оптимизация. Профильный ЕГЭ

Обновлено: 17 мар 2024

Как понять школьный курс химии: полезные советы

Обновлено: 13 май 2024

15 советов по воспитанию ребенка от Медведя из мультика Маша и Медведь

Обновлено: 14 авг 2024

Гипотиреоз у детей: симптомы и лечение

Обновлено: 08 апр 2024