Обратно пропорциональная зависимость
Что такое обратно пропорциональная зависимость? Для данной зависимости должно выполняться условия:
- когда мы увеличиваем одну величину в \(n\) количество раз, то другая уменьшается в точно в такое же количество раз.
- либо если мы увеличиваем одну в \(n\) раз, вторая тоже уменьшается в \(n\) раз.
Рассмотрим ниже примеры решения задач.
Пример 1. Рабочий производит по 42 детали в час на рабочем станке , рабочий затратил время на работу 8 часов. Сколько времени ему надо бы на эту же работу, если бы он производил в час по 48 деталей?
Решение. Составим обратно пропорциональную зависимость:
\(\frac{42}{48}=\frac{x}{8}\)
\(x=\frac{42*8}{48} = 7\)
Ответ: \(7\).
Пример 2. Бассейн полностью наполнятся одной из \(2\) труб. Скорость первой трубы \(2\) литра в \(1\) секунду, бассейн будет полон через \(45\) минут. Вычислите скорость второй трубы, если весь бассейн будет наполнен второй трубой через \(1\) час \(15\) минут.
Решение. Составим обратно пропорциональную зависимость:
\(\frac{120}{х}=\frac{75}{45}\)
\(x=\frac{120*45}{75} = 72\)
Ответ: \(72\).
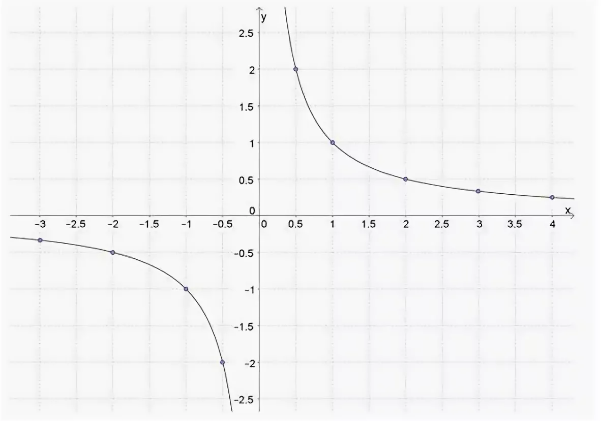
График обратно пропорциональной зависимости
\(y=\frac{k}{x}\)
Наши преподаватели
Репетитор по математике
Стаж (лет)
19
Образование:
Татарский государственный гуманитарно-педагогический университет
Проведенных занятий:
138
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
30
Образование:
Талдыкурганский педагогический институт им. Джансугурова
Проведенных занятий:
163
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
7
Образование:
Уфимский авиационный институт
Проведенных занятий:
282
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор для подготовки к ЕГЭ по физике
- Репетитор по грамматике русского языка
- Репетитор по английскому языку для подготовки к ОГЭ
- Подготовка к олимпиадам по английскому языку
- ВПР по математике
- Репетитор для подготовки к ВПР по английскому языку
- Репетитор по биологии для подготовки к ЕГЭ
- Репетитор по биологии для подготовки к ОГЭ
- Подготовка к ОГЭ по литературе
Похожие статьи
- Параллелограмм
- Математические факты о Чичен-Ица в Мексике
- Основные формулы производной
- Финансовый Университет при Правительстве: Информационная Безопасность
- ЕГЭ по математике, базовый уровень. Преобразование алгебраических выражений
- Как приготовить овощи, каши и мясо, чтобы ребенок их съел
- Интересные факты об устройстве Вселенной
- Как создать лето зимой: растим огород на подоконнике
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так