Парабола: что это, квадратичная функция, построение параболы

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Что такое парабола?
Вершина параболы: формула квадратичной функции
Как определить, куда направлены ветви парабол?
Применение параболы

Обновлено: 13 мар 2024

Парабола: что это, квадратичная функция, построение параболы

Что такое парабола?

Парабола с греческого относится к конкретной плоской Кривой. Слово parabolh означает "сравнение", буквально "бросание рядом".

Вершина параболы: формула квадратичной функции

Мы знаем, что любое линейное уравнение с двумя переменными может быть записано в виде функции \(y=kx+b\) , и что его график является линией. В этой статье мы увидим, что любое квадратичное уравнение вида \(y = ax^2 + bx + c \) имеет изогнутый график, называемый параболой.

Две точки определяют линию. Однако, поскольку парабола изогнута, мы должны найти более двух точек. Найдем по крайней мере пять точек для создания приемлемого графика. Потом построим точки и нарисуем график параболы \(y_1=x^2+2x+3\) по точкам.

Учитывая квадратичное уравнение вида \(y = ax^2 + bx + c \), \(x\) является независимой переменной, а \(y\)-зависимой переменной. Выберем некоторые значения для \(x\), а затем определим соответствующие значения \(y\).

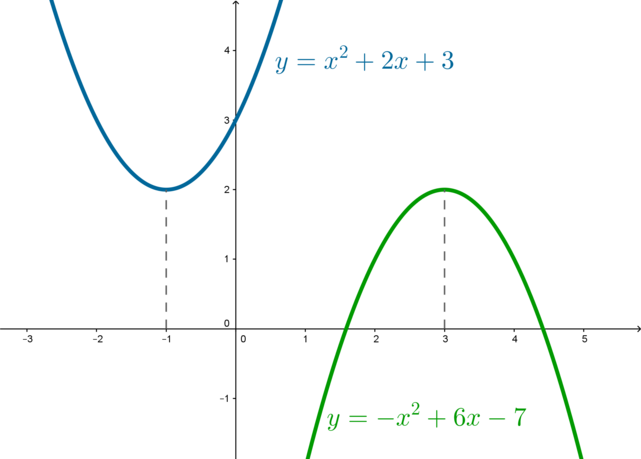
Вывод: графиком квадратичного уравнения \(ax^2 + bx + c = 0\) , где \(a ≠ 0\) является парабола.

Если \(a> 0\), то его вершина указывает вниз.
Если \(a < 0\), то его вершина указывает вверх:
Если \(a = 0 \), то граф не парабола, а прямая линия.

Вершина параболы находится в точке \(x=\frac{ - b}{2a}.\)

На рисунке выше изображены графики парабол \(y_1=x^2+2x+3\) и \(y_2=-x^2+6x-7\). Рассчитаем вершины параболы (формула): \(x_1=\frac{-2}{2*1}=-1\) и \(x_2=\frac{-6}{-2*1}=3.\) Свободный член \(3\) и \(-7\) означает пересечение с осью \(y\), то есть сдвиг графика по оси \(OY.\)

Коэффициент \(b\) означает симметричность относительно оси \(OY.\) Если \(b=0\), то вершина лежит оси \(OY.\)

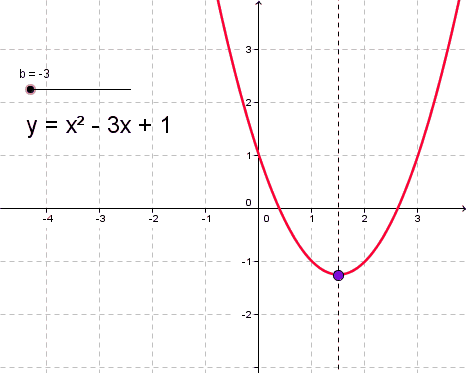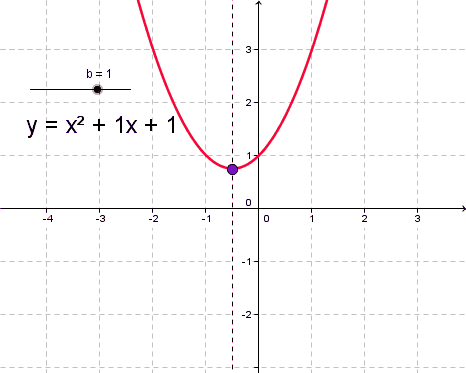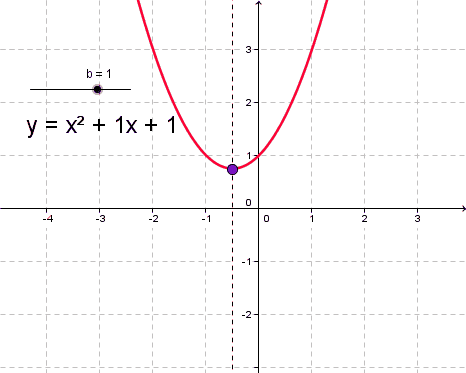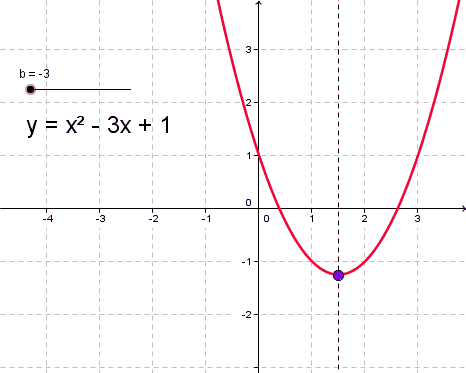
Как определить, куда направлены ветви парабол?

Есть простое правило, по которому можно без построения графика увидеть, когда ветви параболы направлены вниз а когда вверхДля определения направления ветвей параболы, вы должны проанализировать коэффициент перед квадратичным членом уравнения параболы. Уравнение параболы в общем виде имеет вид:

Если коэффициент "a" (коэффициент перед x в квадрате) положителен (a > 0), то ветви параболы направлены вверх. Такая парабола имеет минимум, который находится внизу, а ее значение увеличивается по мере удаления от вершины вниз и вверх.
Если коэффициент "a" отрицателен (a < 0), то ветви параболы направлены вниз. В этом случае парабола имеет максимум в вершине, а ее значение уменьшается по мере удаления от вершины вниз и вверх.

При определении направления ветвей параболы, также полезно посмотреть на знак коэффициента "a", так как он определяет выпуклость или вогнутость параболы.

Применение параболы

Радиоволны часто должна быть сконцентрирована в одной точке например, радиотелескопы, платные телевизионные тарелки, солнечные коллекторы.

Излучение должно передаваться из одной точки в широкий параллельный луч (например, отражатели фар).

Параллельные радиоволны собираются параболической антенной. Параллельные лучи отражаются от антенны и встречаются в точке F, называемой фокусом.

Часто задаваемые вопросы:

✅ Что такое вершина параболы?

↪ Вершина параболы - это точка на параболе, которая находится на равном удалении от фокуса и директрисы. Ее координаты можно найти по формулам \(x = -b/(2a)\) и \(y = c - (b^2)/(4a)\).

✅ Как определить направление ветвей параболы по уравнению?

↪ Направление ветвей параболы зависит от знака коэффициента "a" в уравнении. Если "a" положительный (a > 0), ветви направлены вверх; если "a" отрицательный (a < 0), ветви направлены вниз.

✅ Каково значение дискриминанта уравнения параболы и как он связан с графиком параболы?

↪ Дискриминант уравнения параболы равен \(D = b^2 - 4ac\). Значение дискриминанта определяет тип графика параболы: если D > 0, парабола пересекает ось x в двух различных точках и имеет ветви; если D = 0, парабола касается оси x в одной точке и имеет вершину на оси; если D < 0, парабола не пересекает ось x и не имеет вещественных корней.

Предыдущая статья