Тетраэдр

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Свойства тетраэдра
Виды тетраэдров
Часто задаваемые вопросы:

Обновлено: 05 фев 2024

Тетраэдр

Что такое тетраэдр

Тетраэдр является частным случаем пирамиды т. е. все его грани являются треугольниками, включая основание пирамиды. Как и все пирамиды, тетраэдр представляет собой многогранник — трехмерную геометрическую форму с плоскими гранями и прямыми ребрами. Слово "tetra" берет свое начало в греческом языке и означает четыре, так как у тетраэдра 4 грани.

Тетраэдр имеет:

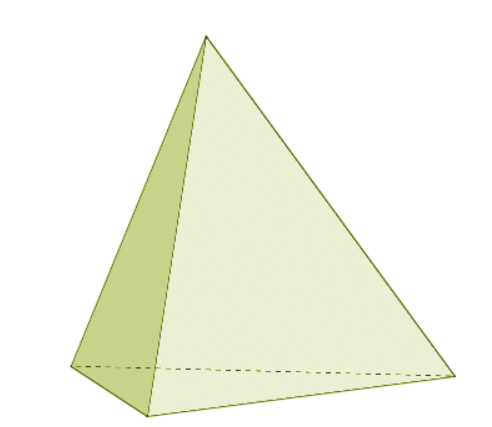
четыре грани;
шесть ребер;
четыре вершины.

Свойства тетраэдра

Как видно из рисунка выше, тетраэдр всегда имеет треугольное основание, любая из четырех граней тетраэдра может быть обозначена как основание, если он правильный.

Все грани тетраэдра являются треугольниками, включая основание. Правильный тетраэдр является частным случаем тетраэдра, для которого все четыре треугольные грани равны, а все внутренние углы равны \(60°\). На рисунке ниже показан равнобедренный тетраэдр.

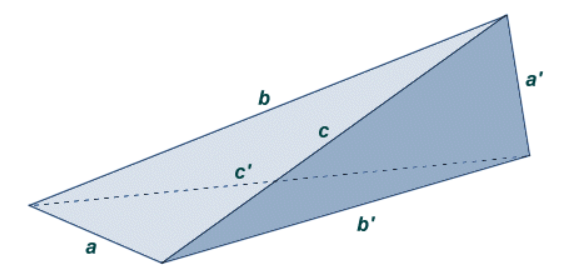
Грани равнобедренного тетраэдра равны.

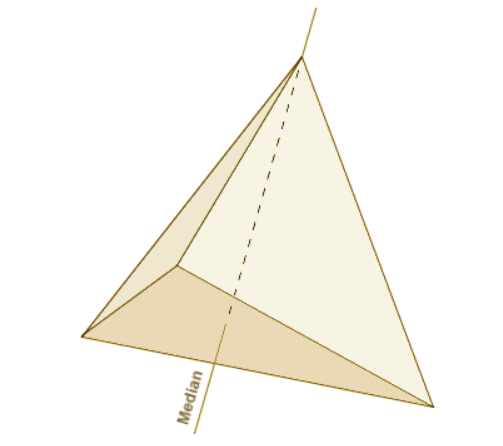
Поскольку все грани правильного тетраэдра являются равносторонними треугольниками, все внутренние углы тетраэдра будут составлять шестьдесят градусов 60°, а сумма углов граней, встречающихся в любой вершине, будет равно 180°. Оси симметрии имеют особое значение, когда мы имеем дело с правильным тетраэдрами. Ось симметрии, которая соединяет вершину правильного тетраэдра с центроидом противоположной грани. По определению, линия, проходящая через любую вершину тетраэдра и центром грани, противоположной этой вершине, называется медианой. Таким образом, тетраэдр имеет четыре 4 медианы.

У правильного тетраэдра каждая медиана совпадает с осью симметрии. Аналогичная ситуация возникает, когда мы рассматриваем ось симметрии, которая соединяет среднюю точку двух противоположных ребер правильного тетраэдра.

Виды тетраэдров

В зависимости от расположения граней и углов между ними существует несколько видов тетраэдров.

Равносторонний тетраэдр - это тетраэдр, у которого все грани равносторонние треугольники, а все углы между ними равны 60 градусам.
Равнобедренный тетраэдр - это тетраэдр, у которого все грани являются равнобедренными треугольниками, то есть имеют две равные стороны, а третья сторона может быть разной длины.
Прямоугольный тетраэдр - это тетраэдр, у которого три грани являются прямоугольными треугольниками, а четвертая грань может быть либо прямоугольным треугольником, либо равносторонним треугольником.
Неправильный тетраэдр - это тетраэдр, у которого все грани имеют разные размеры и формы.

Кроме того, в математике существует понятие расширенного тетраэдра, который состоит из обычного тетраэдра и сферы, которая описывает его грани. Расширенный тетраэдр имеет несколько интересных свойств и применений в различных областях науки.

Часто задаваемые вопросы:

✅ Что такое тетраэдр?

↪ Тетраэдр - это геометрическая фигура, состоящая из четырех треугольных граней, которые соединены в одной общей вершине.

✅ Какие виды тетраэдров существуют?

↪ Существует несколько видов тетраэдров: равносторонний, равнобедренный, прямоугольный и неправильный тетраэдр.

✅ В каких областях науки используются тетраэдры?

↪ Тетраэдры используются в различных областях науки, включая математику, физику, химию и геометрию. Например, тетраэдры могут использоваться для моделирования молекул в химии или для аппроксимации трехмерных объектов в компьютерной графике.

Предыдущая статья