Уравнения с параметром. Задание №18 в ЕГЭ

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Обновлено: 13 янв 2024

Уравнения с параметром. Задание №18 в ЕГЭ

Условие:

Найдите все значения \(a\), при каждом из которых система

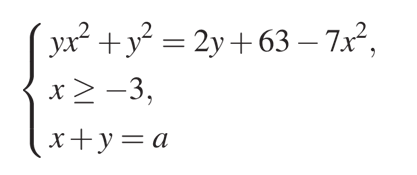
имеет ровно два различных решения.

Решение:

Перед тем, как мы приступим к решению этого задания, необходимо заметить, что нам необходимо указать интервал или конкретное значение \(а\), которое при подстановке в предложенную систему даст именно два различных решения. Теоретически, могут быть и такие значения \(а\), при которых мы сможем получить одно решение, множество решений или не получим ни одного решения. Вот, собственно, все возможные варианты.

Итак, решим первое уравнение относительно \(у\):

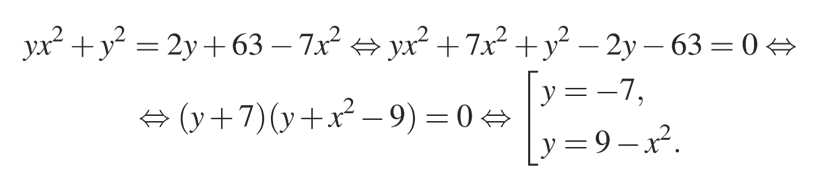
Как видите, мы сначала перенесли правую часть влево. Затем сгруппировали, выделив в первой скобке первые два элемента. А оставшиеся три элемента разложили на множители, как классическое квадратное уравнение. Это позволило нам получить две скобки, связанные знаком умножения и приравненные к нулю. Приравняв к нулю поочередно обе скобки, мы получили два корня.

Именно при двух корнях в решении нам и надо найти значения параметра \(а\).

Если рассмотреть случай (1): \(y = −7\). Для третьего условия системы при любом \(a\) получаем одно решение \(x = a + 7\), для которого второе условие системы, неравенство \(x ≥ −3\) верно только при \(a ≥ −10\).

Если рассмотреть случай (2): \(y=9-x^2\) ⇔ \(9-x^2=a-x\) ⇔ \(x^2-x+(a-9)=0\)

Так как дискриминант при этом получается: \(D=1-4(a-9)=37-4a,\)

то при \(a>9,25\) корней нет (\(D<0\)),

при \(a=9,25\) (\(D=0\)) получаем один корень \(x =0,5\)

а при \(a<9,25\) получаем два различных корня.

Данное квадратное уравнение графически представляет собой параболу.

У параболы \(y=x^2-x+(-9)\) — ветви направлены вверх (коэффициент при \(x^2\) равен 1, 1 > 0), абсцисса вершины равна \(0,5>0\)

Это значит, что оба корня не меньше -3 при \(3+a≥0\) то есть: при \(-3≤a<9,25\), а при \(a<-3\) один корень меньше −3, а другой — больше −3.

Этот анализ позволяет нам собрать сведения о числе решений в случаях (1) и (2) в таблицу:

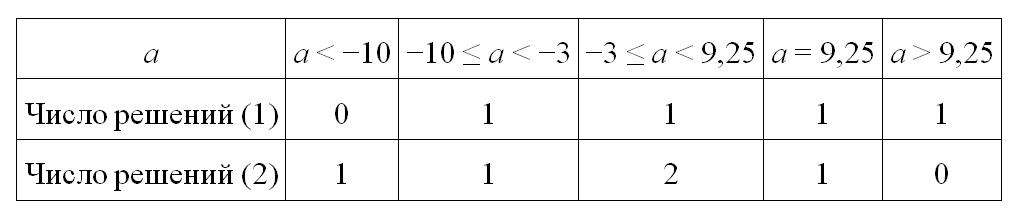
Остаётся учесть те значения a, при которых решение из случая (1) совпадает с одним из решений случая (2).

Тогда из равенства \(-7=9-x^2\) ⇔ \(x = ±4 \) с учётом \(x ≥ -3\) возьмем только \(х = 4\), из \(x+y=a\) получаем, \(a = −3\). Таким образом, к условию \(−10 ≤ a < −3\) добавим \(a = −3\).

Ответ: \(-10≤a≤-3, a=9,25\)

Автор - Андрей Найденов

Предыдущая статья