Хорда. Свойства хорды

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Что такое хорда?
Часто задаваемые вопросы:

17 июн 2024

Хорда. Свойства хорды

Что такое хорда и какие свойства она обладает? Давайте вместе исследуем эти вопросы и откроем для себя интересные законы, связанные с этим понятием.

Что такое хорда?

Хорда окружности - отрезок, соединяющий две точки данной кривой (например, окружность, эллипс, круг, параболы, гиперболы).

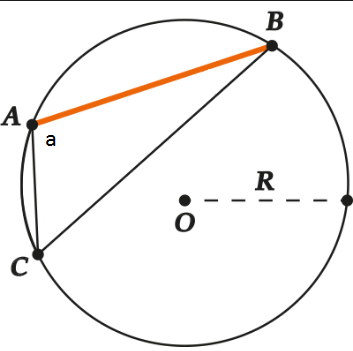
\(CB\) - хорда

Также хорда может описывать отрезки линий, нарисованные на эллипсах и конических сечениях.

Длина дуги - это меньшая длина окружности на которую опирается хорда, обозначается \(◡ AB\).

Свойства хорды

Есть несколько интересных свойств хорд окружности, которые помогают нам лучше понять окружности и использовать их в решении задач. Давайте рассмотрим некоторые из них:

Если длины двух хорд равны, то они лежат на одном расстоянии от центра:
Длину хорды \(AB\) можно вычислить по формуле:

\(AB = 2R sin α\)

Если две хорды равны между собой, то равны и длины этих хорд.

Синус половинного угла будет равен длине хорды, деленный на \(2\) радиуса:

\(sin⁡[\frac{α}{2}]=\frac{AB}{2r}\)

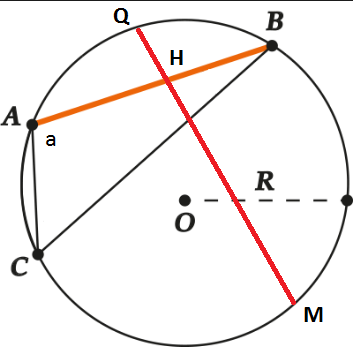
\(AH*HB=QH*HM\)

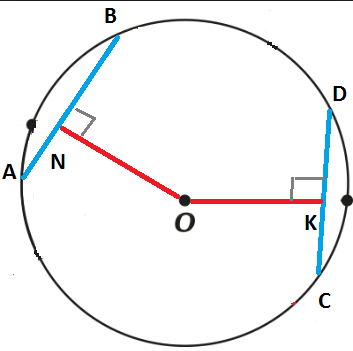
Если \( AB = CD\), то \(ON=OK\)

Диаметр - это хорда, проходящая через центр.

Часто задаваемые вопросы:

✅ Что такое хорда?

↪ Хорда - это отрезок, который соединяет две точки на окружности. Он является прямой линией, которая лежит внутри окружности и имеет конечные точки на ее окружности.

✅ Какие свойства имеет хорда?

↪ У хорды есть несколько важных свойств. Первое свойство - длина хорды меньше диаметра окружности, но больше радиуса. Второе свойство - если две хорды имеют одну и ту же длину, то они находятся на одинаковом расстоянии от центра окружности. Третье свойство - если хорда проходит через центр окружности, то ее длина равна диаметру, а она сама является диаметром окружности.

✅ Как использовать свойства хорды?

↪ Свойства хорды широко используются в геометрии и математике. Они позволяют решать различные задачи, связанные с окружностями. Например, можно использовать свойство хорды для вычисления длины хорды или определения ее расстояния от центра окружности. Также свойства хорды могут быть полезны при изучении углов, касательных и других элементов, связанных с окружностями.

Предыдущая статья