ЕГЭ по математике, профильный уровень. Рациональные уравнения

Андрей Алексеевич рассматривает задачи, которые обязательно встретятся вам в ЕГЭ по математике. Вооружайтесь ручкой, тетрадью и тренируйтесь вместе с нами.

Задание №13

Условие:

а) Решите уравнение

\({{(x-2)^2}\over2}+{{18}\over {(x-2)^2}}={7({x-2\over2}-{3\over x-2})}+10 \)

б) Найдите его корни, принадлежащие отрезку \([-2;2]\)

Решение:

а) Начнем с того, что сделаем замену: "свернем" выражение, заключенное в большие скобки:

\(t={{x-2}\over2}-{3\over x-2}\) ,

Тогда мы сможем левую часть уравнения переписать в следующем виде:

\(t^2={{(x-2)^2}\over 4}+{{9\over (x-2)^2 }}-3\)

Пусть нас не смущает "4" в знаменателе первой дроби, мы сможем выйти из этой ситуации, если запишем вот так:

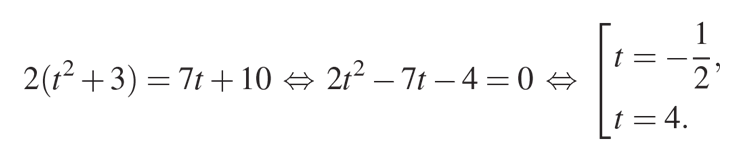
Получилось, что мы преобразовали исходное уравнение в достаточно простую форму, что позволило нам найти два корня.

Вернемся к исходной переменной.

Если \(t=-{1\over2}\) , то

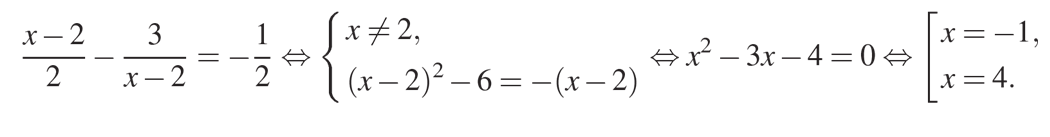
Если \(t=4\) , то

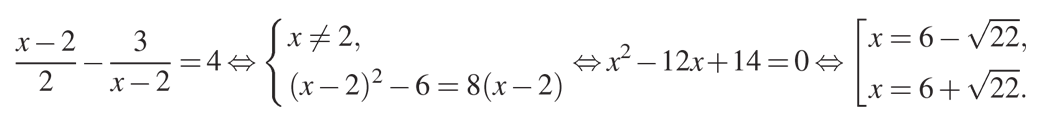
Итак, мы нашли четыре корня, удовлетворяющие исходному уравнению.

б) Выясним теперь, какие из найденных корней принадлежат отрезку \([-2;2]\)

Первый корень "\(х = - 1\)" принадлежит заданному отрезку.

Второй корень "\(х = 4\)" явно не подходит

Давайте оценим третий и четвертый корни:

Корень квадратный из "22", это число, которое меньше "5", так как корень квадратный из "25" равен "5", но больше "4", так как корень квадратный из "16" равен "4".

Тогда справедливы неравенства:

\(0<6-\sqrt22<6-4=2\)

Для третьего корня, и

\(6+\sqrt22>6+4=10>2\)

Для четвертого корня.

Отсюда следует, что из найденных корней уравнения заданному отрезку принадлежат только числа "-1" и "\(6- \sqrt22\)"».

Ответ:

а){ \(-1;4;6- \sqrt22;6+\sqrt22\)}

б) \(-1;6- \sqrt22\)

Автор: Андрей Найденов

Предыдущая статья