Подготовка к контрольной работе по геометрии

 

1.Синус, косинус.  Для любого угла α из промежутка 0°≤α≤180° синусом угла α называется ордината y точки М, а косинусом угла α - абсцисса x точки М.

2. Основное тригонометрическое тождество, формулы приведения. \(sin^2⁡α+cos^2⁡α=1\)    \(sin⁡(90^0-α)=cos⁡α \)    \(cos⁡(90^0-α)=sin⁡α\)  при \(0^0≤α≤180^0\)

\(sin(180°-α)=sin⁡α , \) \(cos⁡(180°-α)=-cos⁡α \) при  \(0°≤α≤180°\)

3. Теорема о площади треугольника. \(S= {1\over2}∙a∙b∙sin⁡C\)

4.Теорема синусов. \({a\over sin⁡A} ={b\over sin⁡B} ={c\over sin⁡C} =2R\)

5.Теорема косинусов. \(a^2=b^2+c^2-2∙a∙b∙cos⁡A\)

6. Скалярное произведение векторов.  \(a ⃗∙b ⃗=|a|∙|b|∙cos⁡(ab)\)                                                       

Если \(a ⃗\){\(x_1;y_1\)}, \(b ⃗\){\(x_1;y_1\)}    \(a ⃗∙b ⃗=x_1∙x_2+y_1∙y_2\)                 

Если  \(a ⃗⊥b ⃗\)   , то   \(x_1∙x_2+y_1∙y_2=0\)         

 

Теперь перейдем к практике. Рассмотрим стандартный вариант контрольной работы для общеобразовательных школ.

 

 

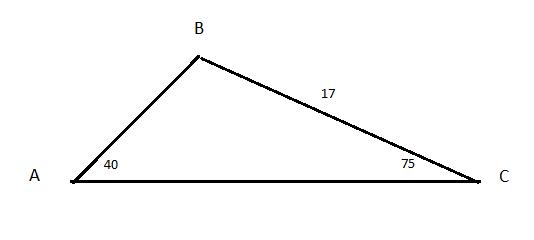
Как видно на чертеже, необходимо найти <B, стороны AB,AC. Найти неизвестные элементы треугольника, значит решить треугольник.

 

Так как известна сторона BC и <A, а они противолежащие, воспользуемся теоремой синусов \({a\over sin⁡A} ={b\over sin⁡B} ={c\over sin⁡C} =2R\) ,                                                  нам пока понадобиться только одна часть \({a\over sin⁡A} ={b\over sin⁡B} \)

 

Мы ее запишем нашим обозначением  \({BC\over sin⁡A} ={AB\over sin⁡C} \)   \({17\over sin⁡40} ={AB\over sin⁡75} \)   из этой пропорции можно найти  AB, но! Чаще всего используются значения  \(sin⁡∝ cos⁡∝\), если \(α=30^0\),\(45^0,60^0,90^0\), а вот как найти \(sin⁡40°, \) \(sin⁡75°\)? Такие значения - причины всех ошибок. Так как эти значения ученик знать не может, и не должен. Для нахождения подобных значений используются таблицы Брадиса Владимира Модестовича, они есть в любой школе, но сейчас их используют редко, так как любой калькулятор может вычислить эти значения. Только следите, чтоб производился ввод в градусах, так как существует еще ввод в радианах. Итак, смотрим, что \(sin⁡40°=0,62\)  \(sin⁡75°=0,97\), эти значения приблизительные, так как на самом деле это бесконечные непериодические дроби.    

 

Итак,  \({17\over 0,62}={AB\over 0,97}\)  отсюда AB= \(AB={{17∙0.97}\over {0.62}}={26.6} \). С помощью отношения \({17\over0,62}=2R\) найдем радиус,  \(R={17\over0,62} :2=13\)

 

Так как нам известны два угла треугольника, то найдем третий \(180-(40+75)=65^0 <B\). Если известен <B и стороны AB и BC , то по теореме косинусов можно найти AC. 

\(a^2=b^2+c^2-2∙a∙b∙cos⁡A\)  для нашего треугольника, она будет выглядеть так \(AC^2=AB^2+BC^2-2∙AB∙BC∙cos⁡B\) 

\(cos⁡65°=0,42\) (смотрим на калькуляторе). Все считаем, не забываем порядок действий и получаем AC²=617 и если уж мы считаем все приблизительно, то √617 тоже считаем на калькуляторе. AC=24,8.

 

Ответ: <B=65⁰, AB=26.6, AC=24,8.

 

И пусть вас не смущает использование калькулятора, по-другому эти задачи решить нельзя. Иногда учителя меняют значения углов на табличные. Тогда, конечно, использовать калькулятор не нужно.

 

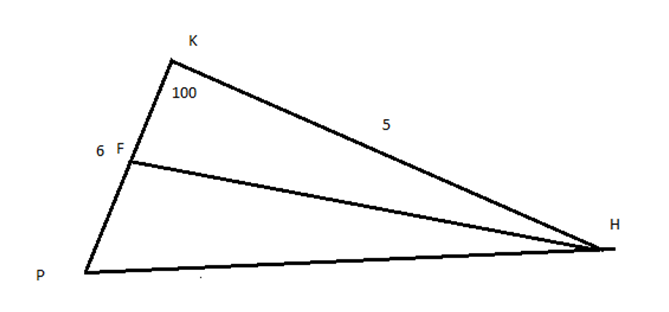
Начинаем с того, что нам дано. FH-медиана, значит т.F делит сторону PK пополам. FP=3

Известны две стороны и угол между ними, значит для стороны, которая лежит напротив угла, применяем теорему косинусов. 

\(PH^2=PK^2+KH^2-2∙PK∙KH∙cos⁡100\)   как видите, нам нужен \(cos⁡100=-0,17\)= (по калькулятору)                                                  

\(PH^2=6^2+5^2-2∙6∙5∙(-0,17)=71,2 \)  \(PK=√71.2=8.4 \) (корень вычисляем по калькулятору). Зная сторону и противолежащий угол, можем воспользоваться теоремой синусов. \({PH\over sin⁡K} ={KH\over sin⁡P} \) . \({8.4\over sin⁡100} ={5\over sin⁡P} \), откуда \(sin P={0.98∙5\over8.4}=0.58 \) и вот тут, чтобы вычислить угол P, нам не всякий калькулятор поможет, нужны таблицы Брадиса. По таблице смотрим  P=35⁰30’ . С другой стороны, чтобы вычислить площадь треугольника, нам нужно знать sin угла, а не то, чему он равен.

 

 

Для нашего треугольника \(S={1\over2}∙FP∙PH∙sin⁡P= {1\over2}∙3∙8.4∙0.58=7.3.\)

Как видим, нам не хватает стороны FH, она же медиана. Находим ее по теореме косинусов \(FH^2=FK^2+KH^2-2∙FK∙KH∙cos⁡100=9+25-2∙3∙5∙(−0.17)=39.1 \) 

\(FH=√39.1=6.3 \) (корень вычислили с помощью калькулятора).

 

Ответ: HF=6.3, S=7.3

 

 

Так как нам не полностью известна координата т. P, у нее y=a, необходимо ее найти. Для этого используем, то, что EK⊥PM.                        

Найдем координаты вектора \(EK ⃗\) {\(1-(-3);4-1\)} от координаты конечной т.K, отнимаем координаты начальной точки E. \(EK ⃗\){\(4;3\)}. Выразим координаты вектора \(PM ⃗\). Выразим, потому что нам не известны все числа. \(PM ⃗\){\(2-(-4);1-a\)}  \(PM ⃗\){\(6;1-a\)}

То, что вектора перпендикулярны, означает, что их скалярное произведение равно 0. Найдем скалярное произведение векторов \(EK ⃗\) и \(PM ⃗\), для этого перемножим их соответствующие координаты.    

\(EK ⃗∙PM ⃗=4∙6+3∙(1-a)=24+3-3a=27-3a=0\)          

Значит \(a=9\), \(PM ⃗\){\(6;-8\)}, \(P(-4;9)\). 

Можно найти угол между прямыми PE и EK. \(cos⁡α={{x_1 x_2+y_1 y_2}\over √x_1^2+y_1^2 ∙√x_2^2+y_2^2}\)

Найдем координаты вектора \(PE ⃗\){\(-3-(-4);1-9\)}   \(PE ⃗\){\(1;-8\)}, а координаты  вектора  \(EK ⃗\){\(4;3\)} нам известны.                                   

Подставим в формулу

 

 

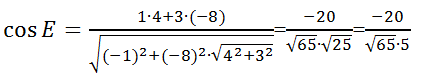
Как видим, известного ответа опять не будет, поэтому считаем значение дроби приблизительно, получаем   \(cos⁡E=-{1\over 2} <E=60^0\), не ровно 60, а чуть больше.

 

Ответ 60⁰15’