Методы решения систем уравнений с двумя переменными

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Решением системы линейных уравнений двух переменных является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.

Как можно решить систему уравнений с двумя переменными?

Системы уравнений с двумя переменными можно решить методом подстановки:

Системы уравнений с двумя переменными можно решить методом сложения:

Пример. Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).

Решение:

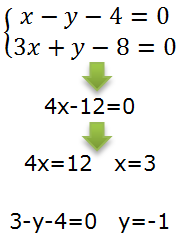
Ответ: \((3;-1).\)

Система уравнений состоящее из двух переменных должно удовлетворять всем решениям одновременно. Система линейных уравнений из двух переменных рассматривается одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, и это будет их решением, другие системы могут иметь бесконечное число решений. Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальное решение.

Выводы:

Система линейных уравнений из двух переменных решается совместно методом подстановки или методом сложения.
Чтобы найти решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям в системе одновременно.
Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных.
Решить систему уравнений это значит найти численное значение для каждой переменной в системе либо доказать что решений нет.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

Методы решения систем уравнений с двумя переменными

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи