Деление столбиком

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Прием деления столбиком
Как делить «с остатком»
Что значит «делить столбиком»
Делим трехзначное число на однозначное
Делим трехзначное число на двузначное
Делим число столбиком с остатком

#Саморазвитие для школьников #Подготовка

26 мар 2024

Деление столбиком

Прием деления столбиком

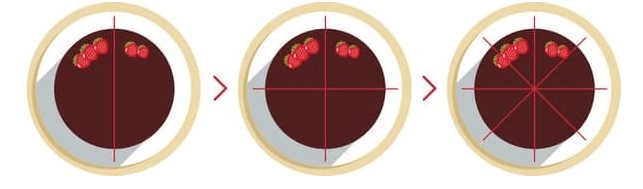
Когда мы говорим о делении, то подразумеваем, что надо нечто целое поделить на несколько одинаковых частей. Допустим, мы хотим поделить торт на восемь человек поровну. Для этого надо порезать торт так, чтобы все восемь кусков оказались одинакового размера.

Источник: paulinecakeclub.ru

Сначала мы режем торт пополам (делим на 2 одинаковые части). После этого каждую половинку режем еще раз пополам (получаем 4 одинаковых куска). И, наконец, делим на 2 одинаковые части каждую четвертинку. В результате получаем 8 одинаковых кусков торта.

Так знание математической операции «деление» помогло нам не обидеть никого из гостей. В повседневной жизни вам придется часто сталкиваться с делением. Например, вы всемером заказали две пиццы, и надо их стоимость поделить на всех.

Мы подскажем, как легко и просто сделать это без помощи взрослых и разных умных гаджетов. Разберемся с операцией деления на примерах для учащихся начальной школы — учеников третьего и четвертого классов. Покажем, как делить числа состоящие из двух или трех знаков.

Как делить «с остатком»

При делении большого числа на маленькое не всегда получается сделать это так, чтобы не было остатка. При этом остаток, получившийся в результате деления, не может быть равен делителю или больше него. Он всегда меньше.

Допустим, мы хотим поделить 18 конфет поровну на 2-х человек. Понятно, что каждому достанется по 9 конфет (18 : 2 = 9). Это пример деления без остатка.

Если же мы захотим поделить 18 конфет на 4-х человек, то каждый получит по 4 конфеты (4 × 4 = 16). И у нас останется еще 2 конфеты — это и будет остаток.

2 < 4. Остаток не превышает делитель и не равен ему — значит, мы поделили конфеты правильно.

18 : 4 = 4 (2). Ответ: 4 и остаток 2.

Что было бы, если бы мы решили дать каждому из четверых человек по 3 конфеты, а не по 4? 4 × 3 = 12. Тогда у нас бы осталось еще 6 конфет (18 − 12 = 6).

Но 6 > 4. Получилось бы, что наш остаток превышает делитель — значит, мы поделили бы неправильно.

Разберем еще два примера.

Разделим 22 на 5. Какое число меньше, чем 22, и при этом делится на 5 без остатка? Это числа 5, 10, 15, 20. Нам нужно выбрать из них самое большое — число 20. Если его поделим на 5, то получим 4. Делаем проверку: 5 × 4 = 20, 22 − 20 = 2. Ответ: 4 и остаток 2. Принято записывать так: 22 : 5 = 4 (2).
Разделим 39 на 6. Самое большое число, кратное 6 и при этом меньше, чем 39 — это 36. 36 : 6 = 6, 39 – 36 = 3. Разделив 39 на 6, мы получим 6 и в остатке будет 3. Запишем решение в виде: 39 : 6 = 6 (3).

Что значит «делить столбиком»

Если вы умеете делить одно число на другое в уме, это замечательно. Но когда числа большие, даже взрослые могут затрудниться это сделать. Чтобы не запутаться при делении больших чисел, математики придумали способ деления столбиком с помощью бумаги и ручки или карандаша.

Мы познакомим вас с алгоритмом деления в столбик. Он очень простой и легко запоминается. После небольшой тренировки вы без затруднения сможете решать похожие примеры самостоятельно.

Делим трехзначное число на однозначное

Давайте разберем, как делить в столбик многозначное число на простом примере: в качестве делимого возьмем трехзначное число 322, а в качестве делителя — однозначное число 7. Необходимо найти частное.

322 : 7 = ?

Приступаем к алгоритму. Каждое действие обозначим отдельными шагами — этапами.

Этап 1. Делимое 322 записываем с левой стороны. Затем рисуем знак уголка. Справа от него записываем делитель. Должно получиться как на картинке внизу.

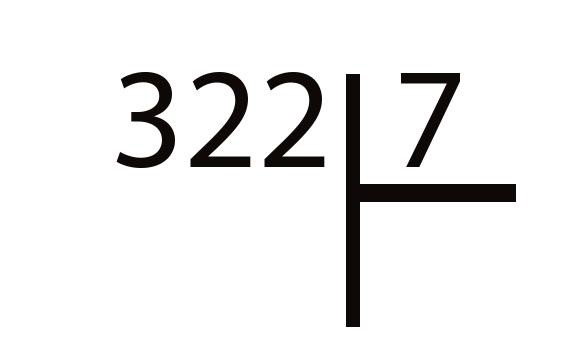
Этап 2. Внимательно изучаем делимое: из скольких сотен, десятков и единиц оно состоит. Нам надо найти число, которое называется «неполным делимым». Оно может оказаться равным делителю или быть больше него.

Число сотен в нашем примере равно 3. Его нельзя поделить на 7, так как 3 < 7. Значит, его мы отбрасываем.

Число десятков у нас — 32. При этом 32 > 7. Значит, оно и будет нашим искомым «неполным делимым».

Делим 32 на 7. Поделить без остатка не получится. Делитель 7 целиком входит 4 раза в делимое 32. Значит, мы нашли неполное частное 4: 7 × 4 = 28, но при этом получили и в остатке 4: 32 − 28 = 4.

Вот как это будет выглядеть в вашей тетради.

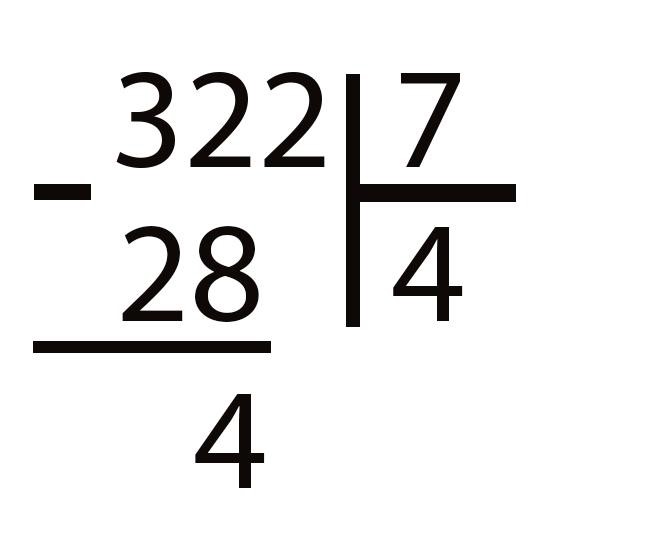
Если бы в качестве неполного частного мы взяли число 5, то нам пришлось бы от 32 отнимать 7 × 5 = 35. Мы не можем отнять 35 от 32, так как вычитаемое не может быть больше уменьшаемого.

Если бы мы рассматривали как неполное частное число 3, то при вычитании мы получили бы в остатке число большее, чем делитель: 7 × 3 = 21, 32 − 21 = 11, 11 > 7. Это решение также было бы ошибочным. Остаток не может быть больше делителя.

Этап 3.

Припишем к полученному остатку с правой стороны следующую цифру делимого. В математике принято обозначать это действие словами «снести двойку». У нас получилось число 42, которое нам нужно продолжить делить на наше делимое 7.

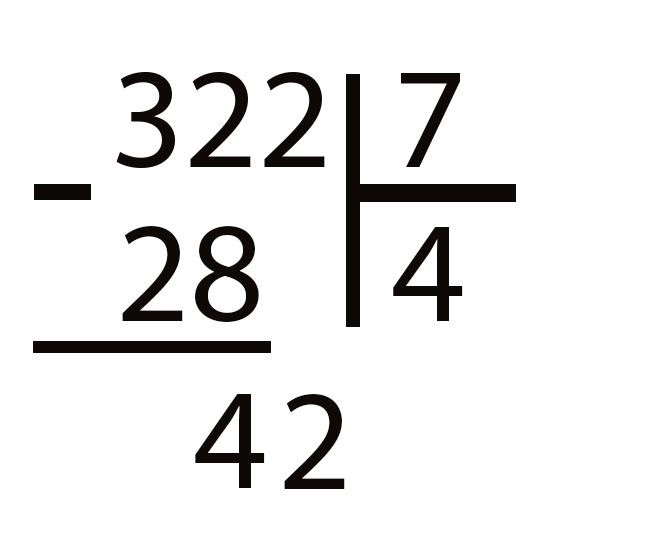
Этап 4. Пробуем получившееся число 42 поделить на 7. Вспоминаем таблицу умножения: 7 × 6 = 42. Значит, 42 делится на 7 без остатка. Пишем рядом с неполным частным 4 (справа от него) цифру 6. Получаем полное частное в виде числа 46.

Пишем внизу: 42 − 42 = 0. Это означает, что число 322 поделилось на 7 нацело, без остатка.

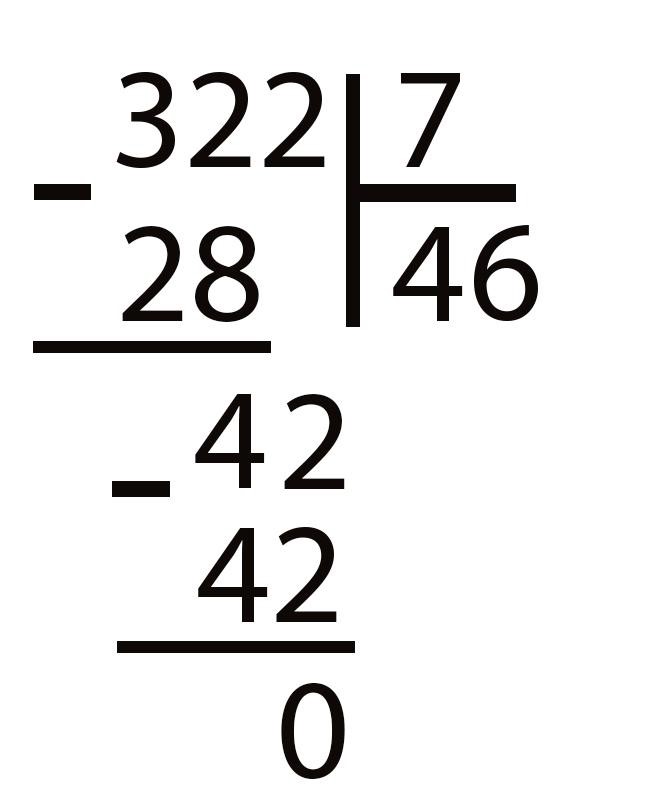
Источник: googleusercontent.com

Ответ: 322 : 7 = 46

Если в результате деления большего числа на меньшее вместо нуля в остатке вы получите какое-то другое число (меньшее, чем делитель), значит оно делится не нацело, а с остатком. И получившееся вместо нуля число и будет этим остатком.

В конце статьи вы найдете задания с ответами, потренировавшись на которых вы легко сможете перейти к следующему уровню.

Делим трехзначное число на двузначное

Если вы достаточно натренировались в делении на однозначные числа, то пора переходить к двузначным, взятым в качестве делителя.

Сначала потренируемся: научимся делить двузначное числа на аналогичное. Попробуем поделить 84 на 14.

84 : 14 = ?

Этап 1. Запишем делимое 84 слева, потом знак уголка, затем справа от него — делитель 14.

Этап 2. Анализируем наше делимое: 8 на 14 поделить нельзя. Будем действовать методом подбора. Найдем, на какое число надо умножить 14, чтобы в результате получилось 84.

14 × ? = 84

Этап 3. По очереди перебираем возможные варианты ответа:

14 × 2 = 28;
14 × 3 = 42:
14 × 4 = 56;
14 × 5 = 70;
14 × 6 = 84.

Последний вариант нас устраивает.

Запишем цифру 6 в качестве частного под знаком уголка с правой стороны:

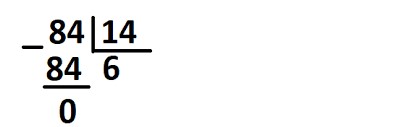
Источник: gstatic.com

Ответ: 84 : 14 = 6.

Теперь рассмотрим более сложный пример: попробуем разделить трехзначное число 273 на число 13, которое является двузначным.

Итак, наше делимое — 273, делитель — 13. Необходимо найти частное.

273 : 13 = ?

Этап 1. Делимое 273 записываем с левой стороны. Затем рисуем знак уголка. Справа от него записываем делитель.

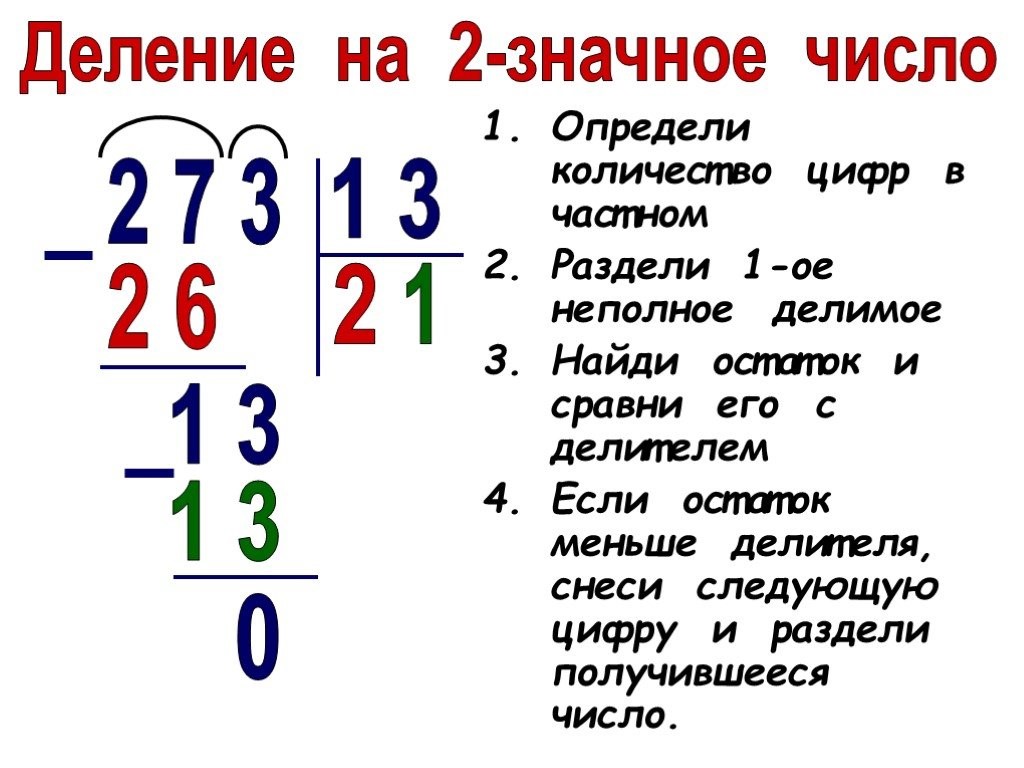
Этап 2. Анализируем наше делимое, как и в предыдущем случае, слева направо. Число 2 на 13 не делится. А вот число 27 нам подходит: 27 > 13. Значит, оно и будет нашим искомым «неполным делимым».

Делим 27 на 13. Поделить без остатка мы не можем. Делитель 13 дважды укладывается целиком в делимое 27. Таким образом, мы нашли неполное частное 2: 13 × 2 = 26, но при этом получаем в остатке единицу: 27 − 26 = 1. Остаток не превышает делитель и не равен ему (1 < 13), значит все в порядке.

Этап 3. Приписываем к полученной единице справа следующую цифру делимого. В нашем случае это цифра 3. Говоря другими словами, «сносим тройку». В результате нас получилось число 13.

Этап 4. Теперь для нас не представляет никакого труда разделить 13 на 13. Любое число делится само на себя без остатка: 13 : 13 = 1. Записываем с правой стороны от неполного частного 2 цифру 1. Получаем полное частное — число 21.

Дописываем наш столбик в самом низу: 13 − 13 = 0. Таким образом, число 273 поделилось на 13 нацело, без остатка.

Возьмем другой пример:

Попробуем поделить трехзначное число 410 на двузначное 82.

410 : 82 = ?

Этап 1. Запишем делимое 410 слева, потом знак уголка, затем справа от него — делитель 82.

Этап 2. Анализируем наше делимое: 4 на 82 поделить невозможно, но и 41 тоже меньше, чем наш делитель 82. Получается, что способ деления столбиком здесь не подходит. Придется действовать методом подбора.

Этап 3. По очереди перебираем возможные варианты ответа:

82 × 2 = 164;
82 × 3 = 246:
82 × 4 = 328;
82 × 5 = 410.

Мы нашли искомое частное путем подбора. Ответ: 410 : 82 = 5.

Делим число столбиком с остатком

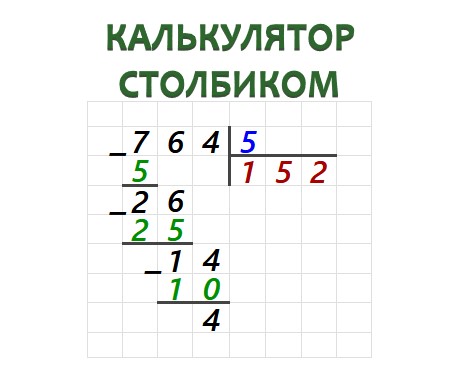
Возьмем трехзначное число 764 и вместе попробуем поделить его на однозначное число 5.

Делимое — 764, делитель — 5. Наша задача — найти частное и проверить, что будет в остатке.

764 : 5 = ?

Действуем по отработанному алгоритму.

Этап 1. Слева записываем делимое 764, рядом с ним рисуем знак уголка, после которого чуть правее записываем делитель 5.

Источник: findhow.org

Этап 2. Анализируем делимое 764 в уже известной нам последовательности. Число сотен 7 больше, чем наш делитель 5. Значит, 7 — наше начальное «неполное делимое».

Делим 7 на 5. Получаем неполное частное 1 и остаток, равный «двойке»: 7 − 5 = 2. Остаток не больше делителя (2 < 5), как и должно быть.

Этап 3. Приписываем к полученной двойке справа следующую цифру делимого. В данном примере это цифра 6. Получаем число 26.

Этап 4. Проделываем всю процедуру еще раз. Ищем самое большее из чисел, делящихся на 5, но при этом меньше, чем 26. Таким числом будет 25 — наш делитель 5 укладывается в него целиком ровно 5 раз: 5 × 5 = 25. Записываем пятерку справа от единицы. 26 − 25 = 1. Все верно — остаток 1 меньше, чем делитель 5.

Этап 5. К полученной в качестве остатка единице сносим четверку — крайнюю из цифер делимого. Получаем число 14, которое надо продолжить делить на 5.

Этап 6. Ближайшее к 14 число, чуть меньше его и делящееся на 5 — это 10. Делим 10 на 5 и получаем 2. Проверяем: 5 × 2 = 10. Двойку приписываем справа в окошке для частного. 14 − 10 = 4. Делаем проверку: остаток 4 < 5. У нас не осталось больше неиспользованных цифр в делимом. Значит, 4 — это конечный искомый остаток. А в окошке для частного — окончательный ответ, искомое частное.

Ответ: 764 : 5 = 152 (4)

Теперь разберем пример деления с остатком трехзначного числа на двузначное.

В качестве делимого возьмем 255, в качестве делителя — 10. Найдем частное вместе с остатком.

255 : 10 = ?

Этап 1. Пишем привычным образом делимое 255 и после знака уголка справа записываем делитель 10.

Этап 2. Рассмотрим делимое 255. Число 2 не подходит по определению (нам нужно число, состоящее не менее чем из двух знаков). Следующее число 25 больше, чем наш делитель 10. Следовательно, оно нам подходит.

Делим 25 на 10. Ближайшее кратное к 10 число — 20. Оно дважды содержит число 10. Таким образом, кроме неполного частного 2 мы получили остаток, равный пяти: 25 − 20 = 5. Остаток не превышает делитель (5 < 10), все верно.

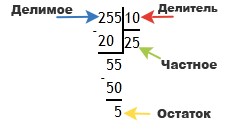
Источник: binary2hex.ru

Этап 3. Сносим вниз к полученной пятерке справа цифру 5, стоящую самой последней в делимом. Мы получили число 55, которое надо разделить на 10.

Этап 4. Продолжаем деление. Наибольшее число, кратное 10, и при этом меньше, чем 55 — это число 50. Наш делитель 10 входит в него 5 раз: 10 × 5 = 50. Записываем пятерку справа от двойки в окошке для записи частного. Проверяем: 55 − 50 = 5. Значит, остаток мы нашли правильно (5 < 10). А число 25 будет искомым частным.

Ответ: 255 : 10 = 25 (5)

Упражнения для самостоятельного деления в столбик

Чтобы убедиться в том, правильно ли вы усвоили материал, стоит немного поупражняться. Попробуйте решить столбиком примеры, приведенные ниже, а потом сверьтесь с нашими ответами.

Начните с легкого (1) уровня: