Свойства равнобедренного треугольника

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Свойства и формулы равнобедренного треугольника
Часто задаваемые вопросы:

Обновлено: 25 авг 2024

Свойства равнобедренного треугольника

Для начала вспомним, что такое равнобедренный треугольник.

Если у треугольника две стороны одинаковой длины, то треугольник зовется равнобедренным.

Свойства и формулы равнобедренного треугольника

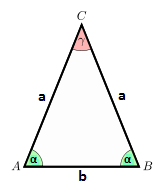
где \(a\)- боковые стороны, \(b\) - основание.

Высота будет и биссектрисой, и медианой. Медиана будет и биссектрисой, и высотой, и биссектриса - высотой и медианой;
Углы α равны;
Площадь треугольника вычисляется:

\(S=(p-b)\sqrt{p(p-a)}\)

\(S=\frac{a}{4}\sqrt{4b^2-a^2}\)

\(S=\frac{b^2}{2}sin γ\)

где \(p\) - полупериметр треугольника, \(a\)- боковая сторона , \(b\) - основание.

Основание \(b\) вычисляется:

\(b=2acos\alpha\)

\(b=2acos(γ/2)\)

Боковые стороны можно найти по формуле:

\(a=\frac{b}{2cos\alpha}\)

\(a=\frac{b}{2sin(γ/2)}\)

Часто задаваемые вопросы:

✅ Что такое равнобедренный треугольник?

↪ Равнобедренный треугольник - это треугольник, у которого две стороны равны между собой, а соответствующие углы при основании также равны.

✅ Какие свойства имеет равнобедренный треугольник?

↪ У равнобедренного треугольника равны основания и боковые стороны, углы при основании равны между собой, а угол при вершине также является равным.

✅ Как вычислить площадь равнобедренного треугольника?

↪ Площадь равнобедренного треугольника можно вычислить, используя формулу: Площадь = (основание * высота) / 2, где основание - одна из сторон треугольника, а высота - перпендикуляр, опущенный из вершины на основание.

Предыдущая статья