img
О платформе Новое Премиум математика Репетиторы Тарифы
Записаться на урок

Дарим первый урок с репетитором бесплатно

Оставьте заявку и получите первый урок в подарок

bg bg gift

Сложение и вычитание отрицательных дробей

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Обновлено: 28 фев 2024

Сложение и вычитание отрицательных дробей

Отрицательные дроби складываются и вычитаются также как и отрицательные числа, только по правилам сложения дробей. Мы можете добавлять только половинки к половинкам, четверти к четвертям или десятые к десятым и так далее. Вычитание отрицательных дробей следует тем же правилам. Для того чтобы сложить или вычесть две дроби нам нужно привести их к общему знаменателю. Если дробь отрицательная мы можем знак минус поставить в числитель и наоборот. Ниже расписано сложение \(-\frac{7}{6}+\frac{5}{7}\):
Сложение отрицательных дробей
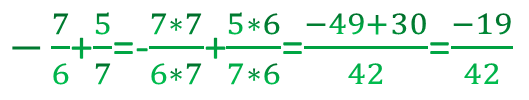
При сложении двух отрицательных дробей результат будет отрицательным. Когда мы вычитаем две отрицательные дроби, то мы к первой отрицательной дроби прибавляем положительную вторую, так как минус на минус дает плюс.
Вычитание отрицательных дробей
 
 
Рассмотрим сложение и вычитание следующих отрицательных дробей.
 
Задача 1. Вычислите \(\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2}).\).
Решение. Приводим к наименьшему общему знаменателю:
\(\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2})=\frac{5-3*2+10}{20}=\frac{9}{20}\)
Ответ: \(\frac{9}{20}\).
 
Задача 2. Вычислите \(\frac{1}{7}-(-\frac{5}{6})-(-\frac{1}{3})\).
Решение. Приводим к наименьшему общему знаменателю:
\(\frac{6-35+14}{42}=-\frac{15}{42}=-\frac{5}{14}\)
Ответ: \(-\frac{5}{14}\).
 
Задача 3. Вычислите \(\frac{1}{4}+\frac{5}{3}-(-\frac{1}{12})\).
Решение. Приводим к наименьшему общему знаменателю:
\(\frac{3+20+1}{12}=\frac{24}{12}=2.\)
Ответ: \(2.\).
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
 
 
 
 
 
 
 
 
 
 
Предыдущая статья img Следующая статья img

Дарим в подарок бесплатный вводный урок!

line gift
Репетиторы arrow
Специализация arrow

Похожие статьи

img

Факультет "Экономика" (НИУ ВШЭ)

Обновлено: 10 фев 2024

 img

Интеграл с переменным верхним пределом

Обновлено: 14 мар 2024

 img

Задачи на движение по окружности

Обновлено: 21 янв 2024

 img

Как вести себя преподавателю со "сложными" детьми

Обновлено: 23 апр 2024

 img

Гигиена зрения: как сохранить здоровье глаз школьника

Обновлено: 23 фев 2024

 img

Школьная газета: для кого, про что и зачем?

Обновлено: 03 июл 2024

 img

Изобретения древности, которыми мы пользуемся сегодня

Обновлено: 09 дек 2023

 img

Калькулятор теоремы Пифагора

11 дек 2023