С 10 до 22.00 по МСК ежедневно
Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок
Основные формулы треугольника
26 май 2024
Основные формулы треугольника
Основные формулы треугольника
В этой статье вы найдете все формулы площадей треугольника:
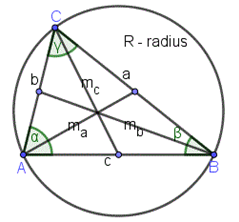
Теорема косинусов
\(a^2=b^2+c^2-2bc* cos α\)
\(b^2=a^2+c^2-2ac* cos β\)
\(a^2=a^2+b^2-2ab* cos γ\)
\(a^2=b^2+c^2-2bc* cos α\)
\(b^2=a^2+c^2-2ac* cos β\)
\(a^2=a^2+b^2-2ab* cos γ\)
Медианные формулы
\(m^2_a=14(2b^2+2c^2-a^2)\)
\(m^2_b=14(2a^2+2c^2-b^2)\)
\(m^2_c=14(2a^2+2b^2-c^2)\)
Формулы биссектрисы
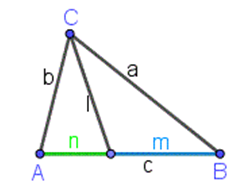
\(\frac{a}{b}=\frac{n}{m}\)
\(l^2=ab-nm\)
\(l^2=ab-nm\)
Прямоугольный треугольник
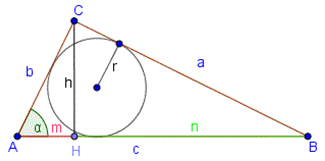
\(c^2=a^2+b^2\)
\(S=\frac{1}{2}ab=\frac{1}{2}ch\)
\(a^2=n⋅с\)
\(b^2=mc\)
\(h^2=m*n\)
\( r=\frac{a+b−c}{2}\)- радиус вписанной окружности
\( sin α=a/c\)
\( tan α=a/b\)
\( cot α=b/a\)
Формулы площади
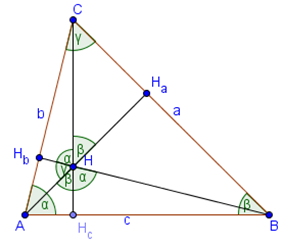
полупериметр \(p=\frac{a+b+c}{2}\)
Площадь треугольника
\(S=\frac{ ch_c}{2}\)
\(S=\frac{ab sin γ}{2}\)
\(S=\sqrt{p(p−a)(p−b)(p−c)}\)
\(S=pr \)
\(S=\frac{ ch_c}{2}\)
\(S=\frac{ab sin γ}{2}\)
\(S=\sqrt{p(p−a)(p−b)(p−c)}\)
\(S=pr \)
где \(r\) радиус треугольника вписанной окружности
\(S=\frac{abc}{ 4R}\)
\(S=\frac{abc}{ 4R}\)
где - R-радиус описанной окружности
Дарим в подарок бесплатный вводный урок!
Репетиторы
![arrow]()
Специализация
![arrow]()
-
![rhombus]()
Подготовка к ЕГЭ по математике (базовый уровень) -
![rhombus]()
Подготовка к ОГЭ по математике -
![rhombus]()
Репетитор для подготовки к сочинению ЕГЭ по русскому -
![rhombus]()
Репетитор по грамматике русского языка -
![rhombus]()
Репетитор по английскому языку для подготовки к ОГЭ -
![rhombus]()
Репетитор по грамматике английского языка -
![rhombus]()
Репетитор по английскому для взрослых -
![rhombus]()
Репетитор по биологии для подготовки к ОГЭ -
![rhombus]()
Программирование Pascal -
![rhombus]()
Scratch
Похожие статьи
Признаки делимости (Часть 1)
26 май 2024
Угол
26 май 2024
Формулы окружности
26 май 2024
Объем прямоугольной призмы
26 июн 2024
РУДН: Геология
26 окт 2024
ЕГЭ по математике, базовый уровень. Задачи на прогрессии
26 янв 2024
Откуда появляются ночные кошмары и почему это нельзя игнорировать
26 окт 2024
Почему многие вкусные продукты вредные?
26 дек 2024