Порядок выполнения арифметических операций

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Как правильно вычислить \(\frac{48}{2}(9+3)\) ? Один получает в ответе \(288\), второй \(2\). В таких случаях стоит помнить, что первое действие выполняется в скобках, и здесь важно знать порядок арифметических операций.

Порядок арифметических операций - это порядок, в котором все алгебраические выражения должны быть выполнены. Зачастую значение выражения меняется в зависимости от порядка его вычисления. Порядок выполнения арифметических операций:

действия в скобках
радикалы, то есть корни
умножение и деление
сложение и вычитание

Круглые скобки - это изогнутые символы \(()\), которые помещаются вокруг части выражения, чтобы показать, что выражения внутри них должны быть вычислены в первую очередь. В круглых скобках следует соблюдать тот же порядок операций. Сначала вычисляются выражения в скобках, затем корни, то есть радикалы, умножение и деление и в конце сложение и вычитание. Если есть несколько одинаковых арифметических операций, то действия выполняются в порядке слева направо.

Пример 1. Вычислить:

Порядок выполнение арифметических операций

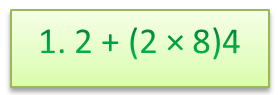
Сначала выполняем умножение в скобках \(2*8=16\), потом деление \(16:4=4\) и затем сложение \(4+1,2=5,2\). В результате выражения получаем \(5,2.\)

Пример 2. Вычислить:

Сначала обратим внимание, что нет скобок и корней, поэтому мы сразу переходим к умножению и делению \(3*3=9\), затем переходим к сложению и вычитанию, работая слева направо \(9-5=4\) и \(4+2=6\) . В результате выражения получаем \(6.\)

Логическое обоснование порядка арифметических операций, помимо скобок, которые, очевидно, являются первыми, заключается в том, что умножение - это повторное сложение, а возведение в степень - это повторное умножение. Кроме того, деление обратно умножению.

Например, выражение:

должно быть решено в следующем порядке: вычисляем выражение в скобках \(6+7=13\), потом выполняем умножение \(2*13=26\) и затем отнимаем от получившегося значения \(82\) и получаем \(-56\). Это и есть наш окончательный результат -56.

Если бы желаемый порядок решения выражения был бы другим, на основе исходной задачи, то скобки были бы расположены по-другому. Порядок операций очень важен, поэтому вы должны понимать порядок арифметических операций на хорошем уровне.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

Порядок выполнения арифметических операций

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи