Положительное и отрицательное направление угла

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

16 июн 2024

Положительное и отрицательное направление угла

Когда два луча выходят из одной точки и при этом не совпадают, они образуют угол.

Углы обычно измеряются в градусах обозначается как \(°\). Углы имеют положительное направление:

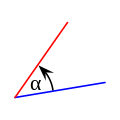
и отрицательное напрвление:

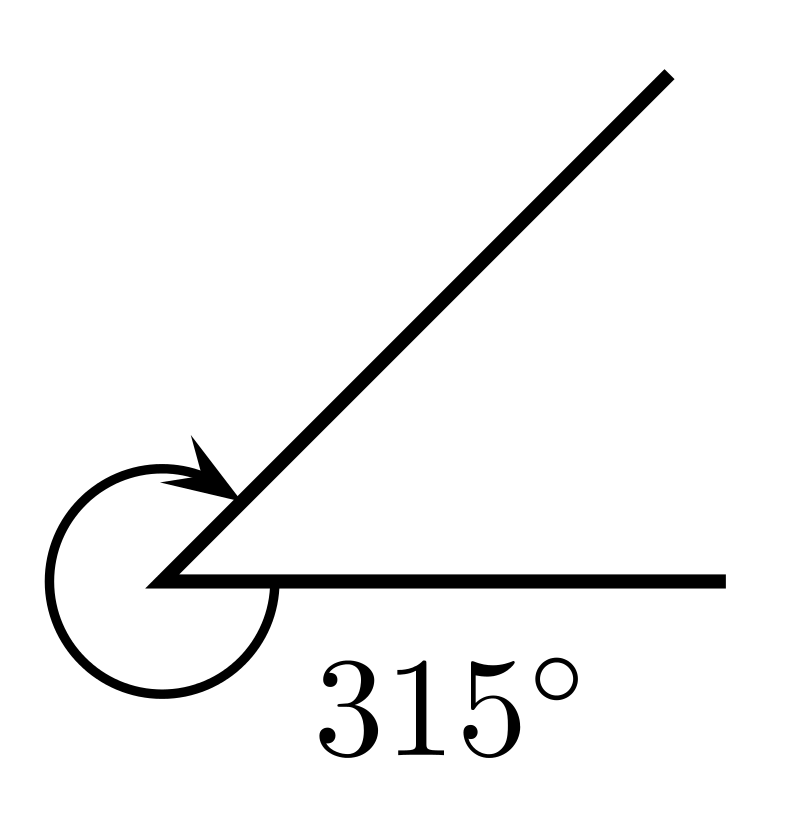
Полный оборот, это когда угол проходит \(360°\). Поэтому один градус это \(\frac{1}{360}\) окружности:

Углы больше 360 градусов

Мы обсуждали, что когда объект совершает один полный оборот вокруг точки, он охватывает \(360°\), однако, когда объект делает более одного оборота, он делает угол больше \(360°\) градусов. Пример явление в повседневной жизни: колеса в машине делают больше одного круга вокруг своей оси, то есть больше чем \(360°\).

Чтобы узнать количество оборотов, сделанных при вращении, мы подсчитываем, сколько раз к нему можно добавить \(360\), чтобы получить число, равное или меньшее заданного угла. Аналогично, мы находим число, которое можно умножить на \(360\) чтобы получить число меньше, но ближе к заданному углу.

Пример 1.
1. Найдите количество оборотов и угол: