Вертикальные углы

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Свойства вертикальных углов
Где можно встретить вертикальные углы в повседневной жизни?
Часто задаваемые вопросы:

Обновлено: 02 фев 2024

Вертикальные углы

В геометрии пары углов могут относиться друг к другу разными способами, в этой статье мы объясним, что такое вертикальные углы.

Когда две линии пересекаются, противоположные углы образуют вертикальные углы или вертикально противоположные углы. Они называются вертикальными углами, так как имеют одну и ту же вершину.

Рассмотрите рисунок вертикальных углов \(y\) и \(y\), \(x\) и \(x\):

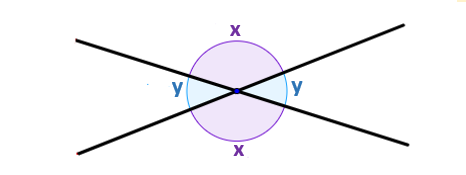
Свойства вертикальных углов

У вертикальных углов есть несколько интересных свойств:

Они имеют одинаковую величину: если мы измерим один вертикальный угол, то второй угол будет иметь ту же самую величину.
Сумма двух вертикальных углов всегда равна 180 градусам. Это свойство называется "сумма вертикальных углов равна 180°".

Вертикальные углы равны. Заметьте также, что сумма углов \(x\) и \(y\) равна \(180°\). Прокрутите страницу вниз для получения дополнительных примеров и решений.

Пример 1. Найти \(x\):

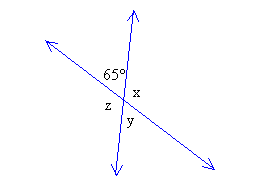
Решение:
\( х + 65° = 180° ⇒ х = 180° – 65° = 115° \)

Найти \(z\):

\(z\) и \(x\) - вертикальные углы, поэтому они равны 115° .

Найти y:

y и \(65°\) вертикальные углы.
Поэтому \(y = 65°\)

Ответ: \(x = 115°, y = 65° , z = 115° \)

Пример 1. \(AEC \) и \(DEB\) прямые линии, которые пересекаются в точке \(E\). \(∠DEC\) \(=135°\). Найти \(q\).

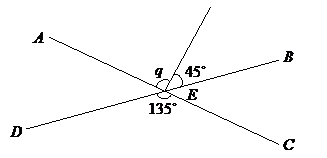
Решение:
\(∠AEB\) = \(∠DEC\) вертикальные углы \(-->\) \( q + 45= 135\)
\(q=\) \( 135 – 45 = 90\)

Где можно встретить вертикальные углы в повседневной жизни?

Вертикальные углы можно найти во многих местах. Например, углы, образованные пересечением углов стола или стула, могут быть вертикальными углами. Также, если вы посмотрите на окна или дверные рамы, вы заметите, что вертикальные углы между вертикальными сторонами рамы также будут равными.

Часто задаваемые вопросы:

✅ Что такое вертикальные углы?

↪ Вертикальные углы - это пара углов, которые образуются при пересечении двух прямых линий и находятся напротив друг друга. Они имеют одинаковую величину и равны друг другу.

✅ Какое свойство имеют вертикальные углы?

↪ Основное свойство вертикальных углов состоит в том, что они имеют одинаковую величину. Если один вертикальный угол равен, например, 50 градусам, то второй вертикальный угол тоже будет равен 50 градусам.

✅ Какова сумма вертикальных углов?

↪ Сумма двух вертикальных углов всегда равна 180 градусам. То есть, если мы сложим меры двух вертикальных углов, получим 180 градусов. Это свойство можно использовать для вычисления одного угла, если известна мера другого вертикального угла.

Предыдущая статья