С 10 до 22.00 по МСК ежедневно
Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок
Умножение и деление дробей
24 апр 2024
Умножение и деление дробей
Любое натуральное число можно представить в виде обыкновенной дроби.
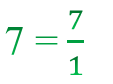
Для того чтобы умножить две дроби надо:
- перевести дроби в неправильные;
- перемножить их числители и записать результат в числитель;
- перемножить их знаменатели и записать результат в знаменатель;
- если можно сократить;
Пример 1. Умножить \(\frac{7}{8}\) и \(\frac{5}{6}\):
При делении дробей вторую дробь нужно перевернуть, то есть поменять местами числитель и знаменатель, а затем выполнить умножение:
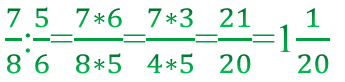
Две дроби называются взаимно обратными, если их произведение равно \(1\).
Пример: 3/4 и 4/3 являются взаимно обратными, так как в результате дают \(1\):
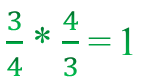
Также стоит помнить, что на ноль делить нельзя.
Задача 1. Умножить \(2\frac{5}{7} \) и \(2 \frac{8}{9}\).
Решение.
\(\frac{19}{7}*\frac{26}{9}\)=\(\frac{494}{63}\)\(=7\frac{53}{63}\)
Ответ: \(7\frac{53}{63}\).
Задача 2. Разделить \(2\frac{5}{6}\) и \(\frac{3}{4} \).
Решение.
\(\frac{17}{6}:\frac{3}{4}\)\(=\frac{17*4}{6*3}=\frac{17*2}{3*3}=\frac{34}{9}=3\frac{7}{9}\)
Ответ: \(3\frac{7}{9}\).
Дарим в подарок бесплатный вводный урок!
Репетиторы
![arrow]()
Специализация
![arrow]()
-
![rhombus]()
Подготовка к ОГЭ по математике -
![rhombus]()
Репетитор по химии для подготовки к ОГЭ -
![rhombus]()
Подготовка к олимпиадам по химии -
![rhombus]()
Репетитор для подготовки к ЕГЭ по физике -
![rhombus]()
Подготовка к олимпиадам по физике -
![rhombus]()
Репетитор по грамматике русского языка -
![rhombus]()
Подготовка к олимпиадам по английскому языку -
![rhombus]()
Репетитор по грамматике английского языка -
![rhombus]()
Репетитор по информатике для подготовки к ЕГЭ -
![rhombus]()
Подготовка к ОГЭ по литературе
Похожие статьи
Переместительное свойство умножения
24 авг 2024
ЕГЭ по математике, профильный уровень. Окружности и четырехугольники
24 сен 2024
ОГЭ по математике. Числа и вычисления
24 май 2024
Как правильно общаться с ребенком об успеваемости?
24 окт 2024
Если мамы нет дома: готовим простые и вкусные перекусы
24 янв 2024
Гипотиреоз у детей: симптомы и лечение
24 янв 2024
Вымершие животные, которые могли существовать, если бы не деятельность человека
24 фев 2024
Калькулятор процентов
24 дек 2024