Производная

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

История дифференциального исчисления
Что такое функция: определение производной
Как находить функцию
Как найти производную функции
Таблицы производной функции
Часто задаваемые вопросы

Обновлено: 01 фев 2024

Производная

История дифференциального исчисления

Дифференциальное исчисление было изобретено Ньютоном и Лейбницем в конце \(17\) века. Это дало мощный толчок в развитии математических исследований. Дифференциальное исчисление радикально изменило математику, как в практических, так и в теоретических вопросах. Операция нахождения производной функции называется дифференцированием.

В учебной программе по естественным наукам и технике дифференциальное исчисление образует мост между элементарной математикой, такой как геометрия, алгебра и тригонометрия, векторный анализ и сложные переменные. Сложные переменные выполняют другие обязанности, помимо простого представления своих элементов. Для начала изучения дифференциальное исчисления необходимо знать понятие функции, непрерывной функции и пределов, а также некоторое представление о природе математического доказательства. В ходе курса вы должны быть ознакомлены с теорией кривых, бесконечных рядов, степенных рядов, элементарных функций и других тем, в качестве примеров, к которым может быть применено исчисление.

Дифференциальное исчисление использует определение производной и свободно использует такие понятия, как дифференциал \(dx\), который отличается от конечной разности Δx. Производная может быть записана \(\frac{dy}{dx}\). Символ \(\frac{dy}{dx}\) используется двояко – как цельный символ производной и как частное дифференциалов.

В самом определении производной в точке подставим на \(x:\)

\(f'(x_0)=\lim\limits_{Δx\to 0} \frac{f(x_o+Δx)-f(x_0)}{Δx}=\lim\limits_{Δx\to 0} \frac{Δy}{Δx};\)

\(f'(x)=\lim\limits_{Δx\to 0} \frac{f(x+Δx)-f(x)}{Δx}=\lim\limits_{Δx\to 0} \frac{Δy}{Δx};\)

Итого функция определяется \(y=f(x)\) по закону:

\(\lim\limits_{Δx\to 0} \frac{f(x+Δx)}{Δx}\)

в соответствии другой функции \(y'=f'(x)\), которая называется производной функцией или просто производной.

Что такое функция: определение производной

Функция – это особый математический объект, который связывает между собой два числа. Один из этих чисел называется аргументом, а другой – значение функции. Функцию можно представить себе как машину, которая получает на вход число и выдаёт на выход другое число.

Производная функции – это понятие, которое используется для определения скорости изменения значения функции при изменении аргумента. Другими словами, производная функции показывает, насколько быстро меняется значение функции при изменении аргумента.

Как находить функцию

Как находить функцию? Для начала нужно понимать, что функцию можно задать формулой. Например, функция y = 2x + 1 означает, что значение функции y равно удвоенному значению аргумента x, увеличенному на единицу. Такую функцию можно нарисовать на графике, где по оси x откладываются значения аргумента, а по оси y – значения функции.

Чтобы находить значения функции по заданной формуле, нужно подставлять значения аргумента вместо x и вычислять значение функции.

Например, если нужно найти значение функции y = 2x + 1 при x = 3, то нужно подставить вместо x число 3 и вычислить: y = 2 * 3 + 1 = 7. Таким образом, значение функции при x = 3 равно 7.

Как найти производную функции

Как найти производную функции? Существует несколько способов. Один из них – использование формулы для производной. Например, если дана функция y = x^2, то ее производная будет равна 2x. Это означает, что при увеличении аргумента на единицу значение функции будет увеличиваться в два раза.

Еще один способ – использование графика функции. Производная функции в точке определяется как тангенс угла наклона касательной к графику функции в этой точке. Если график функции имеет положительный наклон в данной точке, то производная будет положительной, а если отрицательный – то производная будет отрицательной.

Знание функций и их производных поможет решать множество задач в математике и других областях знаний. Например, функции используются для моделирования различных процессов в физике, экономике и других науках. Поэтому важно учиться находить функции и их производные, чтобы лучше понимать мир вокруг нас и решать задачи в будущем.

Таблицы производной функции

Выведены таблицы производных элементарных функций, включающие тригонометрические, гиперболические, логарифмические и экспоненциальные функции, которые надо выучить.

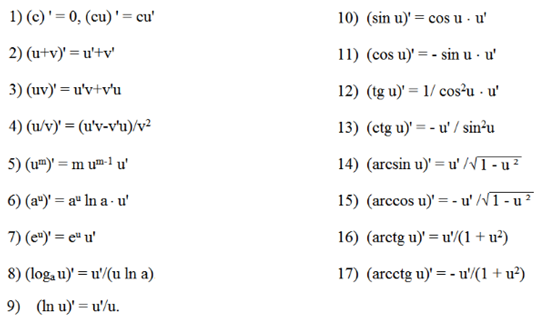
Производная константы всегда равна нулю, то есть производная любого числа равна \(0.\)

Таблица производных 2:

Пример 1. Производная \(2x^2=2*2x^{2-1} =4x\) или \(5x^3=5*3x^{3-1}=15x^2\) по правилу \((x^n)'=nx^{n-1}.\)

Производная \(ln(2x^2)'=\frac{1}{2x^2}*(2x^2)'=\frac{4x}{2x^2}=\frac{2x}{x^2}=\frac{2}{x}\).

Пример 2. Вычислить производную \(5x^{\frac{3}{5}}.\). Решение:

\(y'=(5x^{\frac{3}{5}})'=5*\frac{3}{5}x^{\frac{3}{5}-1}=3x^{-\frac{2}{5}}\)

Ответ: \(3x^{-\frac{2}{5}}\).

Пример 2. Вычислить производную \(\frac{2x^3}{x^{\frac{1}{3}}}\). Решение:

\(y=\frac{2x^3}{x^{\frac{1}{3}}}=2x^{3-\frac{1}{3}}=2x^{\frac{8}{3}};\)

\(y(2x^{\frac{8}{3}})'=2*\frac{8}{3}x^{\frac{8}{3}-1}=\frac{16}{3}x^{\frac{5}{3}}\)

Ответ: \(\frac{16}{3}x^\frac{5}{3}\).

Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.

Часто задаваемые вопросы

✅ Что такое производная функции?

↪ Производная функции – это понятие, которое используется для определения скорости изменения значения функции при изменении аргумента.

✅ Как найти производную функции?

↪ Существует несколько способов, один из них – использование формулы для производной. Другой способ – использование графика функции.

✅ Зачем нужно знать производные функций?

↪ Знание функций и их производных помогает решать множество задач в математике и других областях знаний, таких как физика и экономика. Функции используются для моделирования различных процессов, поэтому важно учиться находить функции и их производные, чтобы лучше понимать мир вокруг нас и решать задачи в будущем.

Предыдущая статья