Задачи на вклады в банк
Условие:
Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн рублей, где х — целое число. Найдите наименьшее значение «х», при котором банк за четыре года начислит на вклад больше 7 млн рублей.
Решение
Проведем небольшой анализ условия задачи. Если у нас в год вклад увеличивается на 10%, то в конце первого года вклад составит 11 млн рублей, а в конце второго — 12,1 млн рублей ( 11 + 1,1). В начале третьего и четвертого года вкладчик пополняет вклад на «х» рублей. Получается, что в начале третьего года вклад (в млн рублей) составит 12,1 + х, а в конце — 13,31 + 1,1х. Аналогично, в начале четвёртого года вклад составит 13,31 + 2,1х, а в конце четвертого года — 14,641 + 2,31х.
Так как по условию задачи нам необходимо найти наименьшее целое х, для которого только начисления банка составят 7 млн рублей, то для него должно быть выполнено неравенство:
(14,641 + 2,31х) – (10 + 2х) > 7
В котором первая скобка представляет собой весь процесс движения средств по счету за четыре года, а вторая скобка представляет собой сумму денег, которые вкладчик внес на счет за все четыре года.
Решим данное неравенство, раскрыв скобки и приведя подобные и получим:
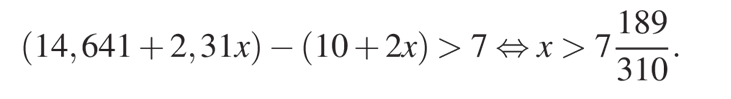
Получается, что наименьшее целое решение этого неравенства — число 8. Таким образом, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на 8 млн рублей.
Ответ: 8
Автор - Андрей Найденов
Наши преподаватели
Репетитор по математике
Стаж (лет)
21
Образование:
Пермский государственный национальный исследовательский университет
Проведенных занятий:
1026
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Подготовка к ОГЭ.
Любите ли Вы математику так, как люблю ее я? Я поделюсь с Вами этим чувством, ведь математическая дисциплина не только интересна и полезна, от нее можно получить истинное удовольствие. Математика ценит настойчивость и терпение, за которые щедро вознаграждает. Благодаря точным наукам можно почувствовать себя настоящим волшебником, великим ученым и смелым первооткрывателем! Дифференцированное обучение, помноженное на доброжелательность и ответственность, помогут возвести в положительную степень уверенность ученика в своих силах и в способностях к математике. Присоединяйтесь! Вместе мы - сила!
Репетитор по математике
Стаж (лет)
21
Образование:
Могилевский государственный университет им А.А. Кулешова
Проведенных занятий:
1216
Форма обучения:
Дистанционно (Скайп)
Репетитор 8-11 классов. Занимаюсь подготовкой к сдаче ОГЭ, ЕГЭ. В преподавании считаю самым главным комфортную атмосферу и доверие. Помогаю ученикам не бояться ошибок. Считаю, что умение помочь ученику поверить в свои силы, увидеть свой потенциал - это миссия каждого учителя!
Репетитор по математике
Стаж (лет)
2
Образование:
Казанский федеральный университет
Проведенных занятий:
0
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку для 1-7 классов и по французскому языку для 4-11классов. Обучаю прекрасному французскому языку с нуля и помогаю совершенствовать его всем желающим (от 1 до 11 класса). Также могу помочь сдать 'экзамен DELF. Будем прорабатывать все языковые навыки и речевые умения. На занятиях не исключён билингвизм (двуязычие - французский + английский). Доступны уроки и английского языка в 1-7 классах. Опыт работы - более 2193 часов.