Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Как по координатам вершин треугольника записать уравнения сторон и уравнение биссектрисы
Условие:
По известным координатам вершин треугольника А(4;4), В(-6;-1), С(-2;-4) записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла АВС.
Решение
Так как нам известны координаты вершин, то проще всего получить уравнение стороны в канонической форме – формула, от которого легко перейти к уравнению в общей форме. Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).
1. Найдем уравнение стороны АВ. В качестве точки прямой можно взять точку А с заданными координатами, а в качестве направляющего вектора – вектор АВ. Найдем координаты вектора АВ:
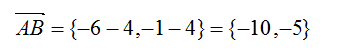
2. Тогда каноническое уравнение стороны АВ запишется:
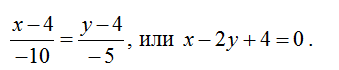
3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны ВС: координаты вектора
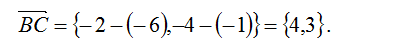
4. Откуда каноническое уравнение: 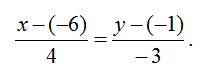
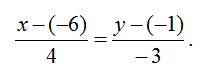
Следовательно, общее уравнение: 3x+4y+22=0.
5. Для стороны CА: координаты направляющего вектора 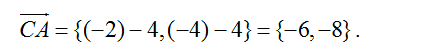
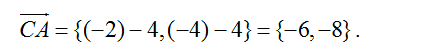
6. Каноническое уравнение: 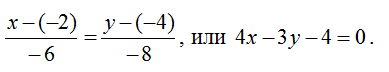
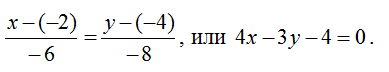
7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах АВ и ВС треугольника отложить орты (соответственно a и b) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов a и b).
8. Для нахождения орта a необходимо знать координаты вектора BA:
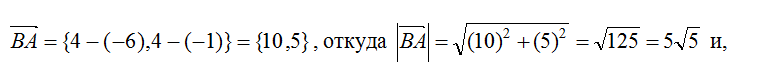
соответственно a определится как:
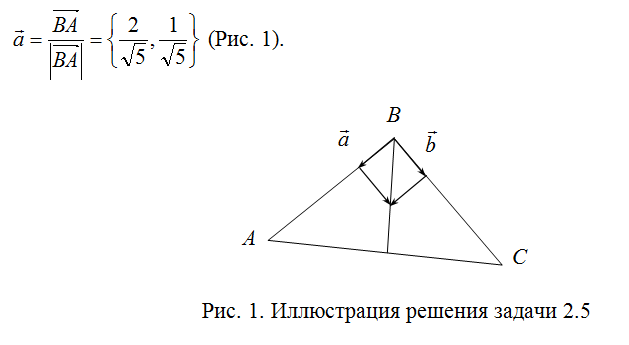
9. Аналогично определим орт b:
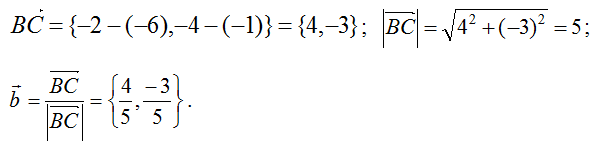
Теперь определим их сумму:
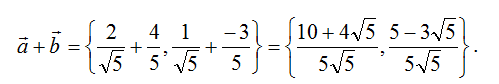
10. Тогда каноническое уравнение биссектрисы:
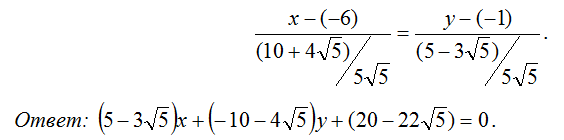
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Репетитор по олимпиадной математике
Репетитор по олимпиадной математике -
 Репетитор для подготовки к ЕГЭ по химии
Репетитор для подготовки к ЕГЭ по химии -
 Подготовка к олимпиадам по химии
Подготовка к олимпиадам по химии -
 Репетитор для подготовки к ЕГЭ по физике
Репетитор для подготовки к ЕГЭ по физике -
 Репетитор по грамматике английского языка
Репетитор по грамматике английского языка -
 Репетитор по истории ОГЭ
Репетитор по истории ОГЭ -
 Подготовка к ВПР по английскому
Подготовка к ВПР по английскому -
 Репетитор по обществознанию ВПР
Репетитор по обществознанию ВПР -
 Репетитор для подготовки к ЕГЭ по географии
Репетитор для подготовки к ЕГЭ по географии -
 Программирование Pascal
Программирование Pascal


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

