Медиана треугольника

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Медиана в равнобедренном треугольнике
Свойства медианы

Что такое медиана треугольника?

Медиана треугольника — это отрезок, соединяющий вершину треугольника c серединой противоположной стороны. Прямая тоже может быть медианой. Треугольник имеет три стороны, поэтому у него всегда ровно три медианы, каждая из которых выходит из вершины к середине противоположной стороны треугольника.

Что такое

Давайте введем определение высоты:

Для построения медианы необходимо:

найти середину стороны и обозначить ее точкой;
соединить найденную точку с противолежащей вершиной треугольника.

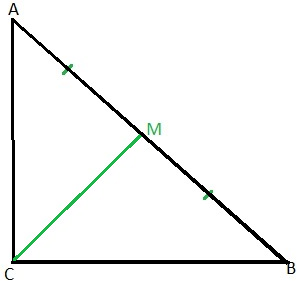
Медиана в равнобедренном треугольнике

Напомним про свойства равнобедренного треугольника из теоремы:

Если мы проведем медиану к основанию в равнобедренном треугольнике, то увидим что она также является и высотой:

Напомним, что такое биссектриса:

Все медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2 к 1.

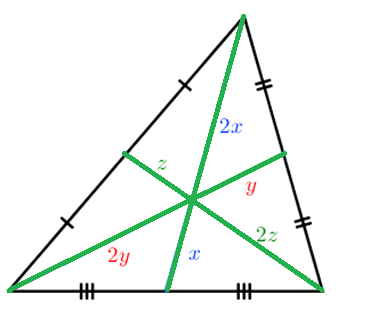
Свойства медианы

Медиана - это значение, которое делит упорядоченный набор данных на две равные части, то есть 50% значений находятся выше медианы, а 50% - ниже. Вот некоторые свойства медианы:

Медиана не зависит от выбросов в данных. Это означает, что если в наборе данных есть несколько значений, которые являются выбросами (то есть существенно отличаются от остальных значений), то медиана останется той же самой.
Медиана может быть использована для измерения центральной тенденции. В отличие от среднего значения, медиана более устойчива к выбросам и не будет искажена ими.
Если набор данных имеет четное количество значений, то медианой будет среднее значение двух средних элементов. Если же набор данных имеет нечетное количество значений, то медианой будет средний элемент.
Медиана может быть использована для определения дисперсии. Дисперсия - это мера распределения данных вокруг центральной тенденции. Медиана может быть использована для определения интерквартильного размаха, который является мерой разброса данных вокруг медианы.
Медиана может быть использована для определения выбросов. Если значение в наборе данных существенно отличается от медианы, то оно может быть классифицировано как выброс.
Медиана может быть использована для проверки симметричности распределения. Если медиана равна среднему значению, то распределение является симметричным. Если же медиана смещена вправо или влево от среднего значения, то распределение считается асимметричным.

Задача 1:

В равнобедренном треугольнике медиана, исходящая из вершины, которая не является вершиной угла с наименьшей мерой, равна 12 см. Найдите боковую сторону треугольника.

Ответ:

Ответ: 12 см. В равнобедренном треугольнике медиана, исходящая из вершины, которая не является вершиной угла с наименьшей мерой, равна половине основания треугольника, т.е. равна боковой стороне треугольника.

Задача 2

В треугольнике ABC медиана, проведенная из вершины А, равна 8 см, а медиана, проведенная из вершины B, равна 6 см. Найдите длину медианы, проведенной из вершины C.

Ответ: 10 см. В треугольнике ABC медиана, проведенная из вершины А, делит сторону BC пополам, а медиана, проведенная из вершины B, делит сторону AC пополам. По свойству медиан треугольника, точка их пересечения делит каждую медиану в отношении 2:1. Значит, медиана, проведенная из вершины C, делит сторону AB в отношении 2:1, т.е. длина медианы из вершины C равна 10 см.

Задача 3

В треугольнике ABC медиана, проведенная из вершины А, равна 6 см, а медиана, проведенная из вершины B, равна 8 см. Известно, что периметр треугольника равен 30 см. Найдите длину стороны AB.

Ответ: 8 см. Рассмотрим треугольник ABC. По свойству медиан треугольника, медиана, проведенная из вершины А, делит сторону BC пополам, а медиана, проведенная из вершины B, делит сторону AC пополам. Значит, длины сторон BC и AC равны соответственно 2 * 6 = 12 см и 2 * 8 = 16 см. Так как периметр треугольника равен 30 см, то длина стороны AB равна 30 - 12 - 16 = 2 см. Таким образом, сторона AB равна 2 см, а медиана, проведенная из вершины C, делит эту сторону пополам, значит, ее длина равна 8 см.