Задачи по планиметрии

Условие:
 
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что СМ=\(1 \over 2\)DK
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
 
Решение
 
 
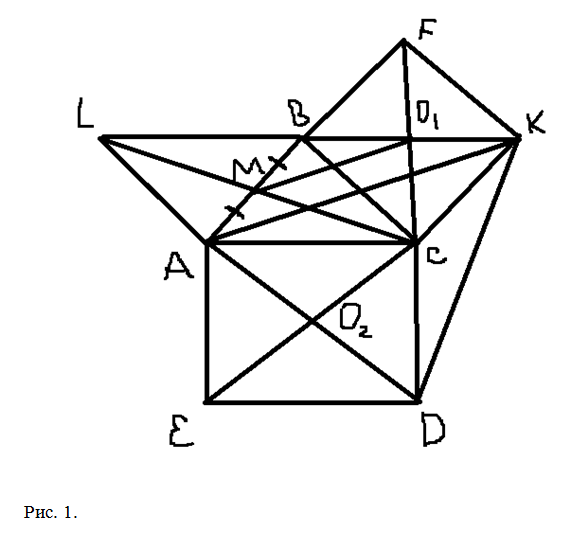
а) Построим треугольник и два квадрата, как требуется в условии задачи (рис.1). Достроим треугольник ABC до параллелограмма ALBC, тогда точка M  является точкой пересечения его диагоналей.
В треугольнике LAC:
 
∠LAC=180°-∠ACB=∠KCD
 
По построению, получается:
AL = BC = KC 
AC = CD.
Тогда мы видим, что треугольники LAC и KCD равны по двум сторонам и углу между ними.
Откуда LC = KD, а СМ:
 
CM=\(1\over 2\)LC=\(1\over 2\)KD
 
что и требовалось доказать.
 
 б) Сделаем дополнительные построения. Соединим точки А и К. Проведем диагонали в квадратах. Пусть O1 — центр квадрата CKFB. Тогда MO1 — средняя линия треугольника AKB. Найдем теперь AK по теореме косинусов из треугольника ACK.
 
 
 
Откуда:   MO=  \(1\over 2\)*38=19
 
Расстояние МО2 можно найти, используя такой же алгоритм. Таким образом, расстояние от М до О2 сведется к нахождению DB.
Это расстояние будет таким же как и MO1 .
 
Ответ:19.
 
Автор - Андрей Найденов
 
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Тамара Анатольевна Меркулова
Репетитор по математике
Стаж (лет)
35
Образование:
МФТИ
Проведенных занятий:
3167
Форма обучения:
Дистанционно (Скайп)
Галина Павловна Симакова
Репетитор по математике
Стаж (лет)
22
Образование:
Пермский государственный национальный исследовательский университет
Проведенных занятий:
1474
Форма обучения:
Дистанционно (Скайп)
Александр Федорович Каморников
Репетитор по математике
Стаж (лет)
24
Образование:
Гомельский государственный университет им. Ф. Скорины
Проведенных занятий:
1128
Форма обучения:
Дистанционно (Скайп)
Предметы
Специализации
Похожие статьи