Как возвести комплексное число в n-ую степень

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Комплексные числа: формулы
Часто задаваемые вопросы:

Обновлено: 04 июн 2024

Как возвести комплексное число в n-ую степень

Комплексное число имеет три формы записи: алгебраическая форма записи Z=a+bi, показательная и тригонометрическая форма записи.

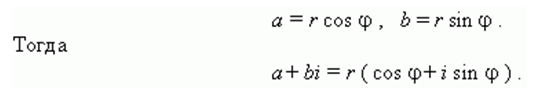
Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается |a+ bi | или буквой r и равен:

\(r=|a+bi|= = { \sqrt{a^2+b^2}}\)

Сопряжённые комплексные числа имеют одинаковый модуль.

Аргумент комплексного числа - это угол φ между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan φ = b / a . Далее рассмотрим, как найти аргумент комплексного числа.

Пусть \(z=a+bi, r=|z|={\sqrt{a^2+b^2}}\) и φ = arg z. Тогда по определению аргумента имеем:

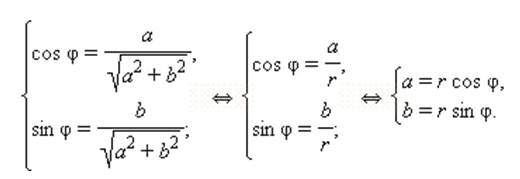
Отсюда получается:

z = a + bi = r(cos φ + i sin φ).

Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа в степени к тригонометрической форме, нужно найти его модуль и один из аргументов.

Записать число \(z=1-{\sqrt3i}\) в тригонометрической форме

Решение:

Найдем модуль этого числа: \(|z|={\sqrt{{1^2}+{(\sqrt3})^2}}={\sqrt {1+3}}=2\)

Аргумент данного числа находится из системы:

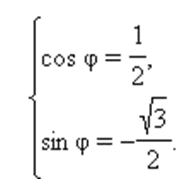
Значит, один из аргументов числа \(z=1-{\sqrt3i}\) равен \(-{π\over3}\)

Получаем:

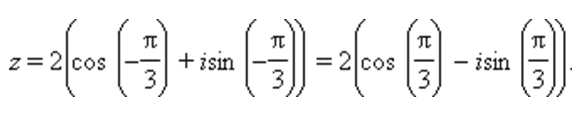
Комплексные числа: формулы

Операции с комплексными числами в тригонометрической форме:

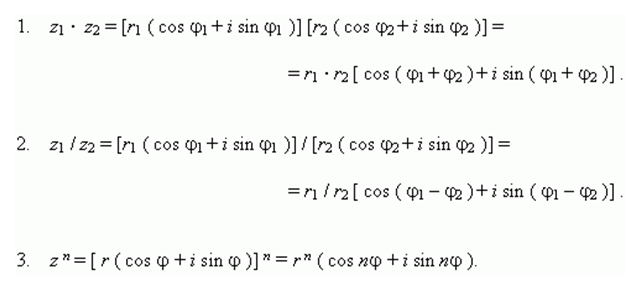
Последняя формула называется формулой Муавра и используется для возведения комплексного числа в n-ую степень.

Автор - Дмитрий Айстраханов

Часто задаваемые вопросы:

✅ Как возвести комплексное число в n-ую степень?

↪ Для возведения комплексного числа в n-ую степень нужно возвести его модуль в степень n, а аргумент умножить на n. Затем полученное значение нужно представить в показательной форме комплексного числа.

✅ Как вычислить степень комплексного числа, если n - целое число?

↪ Если n является целым числом, то можно использовать формулу де Муавра. Сначала нужно записать комплексное число в тригонометрической форме, затем возвести его модуль в степень n, а аргумент умножить на n. Результат представляет собой комплексное число в тригонометрической форме.

✅ Как вычислить степень комплексного числа, если n - нецелое число?

↪ Если n является нецелым числом, то можно использовать формулу Эйлера. Сначала нужно записать комплексное число в показательной форме. Затем возвести модуль в степень n и умножить аргумент на n. Результат представляет собой комплексное число в показательной форме.

Предыдущая статья