ЕГЭ по математике, профильный уровень. Иррациональные неравенства

Условие:
 
Решите неравенство:
 
 
 
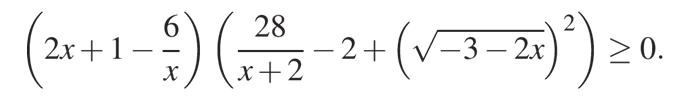
Решение:
 
Как мы видим, в этом примере присутствует квадратный корень, что и делает это неравенство иррациональным. Мы обязательно должны учесть, что выражение под корнем должно быть неотрицательным. После этого мы можем избавиться от иррациональности, если возведем этот корень в квадрат, который, кстати, уже так и стоит в этом примере. Получается, что данное неравенство будет эквивалентно следующей системе неравенств:
 
 
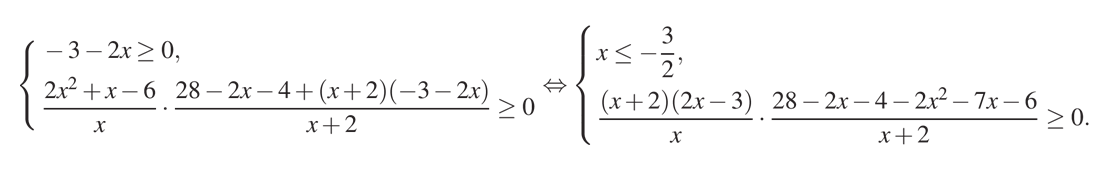
Согласитесь, что в таком виде, после преобразований, работать с этим неравенством стало намного удобнее.
 
Второе неравенство в этой системе удобно решить методом интервалов, учитывая ограничения, накладываемые выражением "х + 2", стоящим в знаменателе. Ограничение "х не равно нулю" не актуально, так как выше мы определили для этого неравенства другое условие, при котором "х меньше или равен -3/2". Запишем второе неравенство и преобразуем его:
 
 
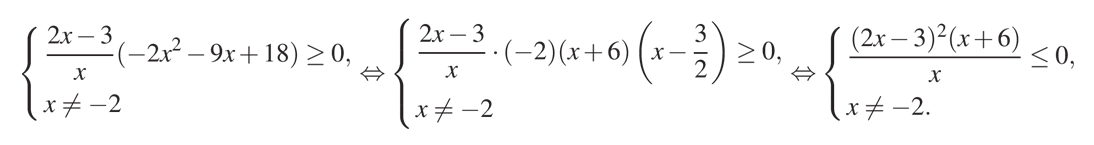
Мы получили в числителе выражение, которое позволяет определить знаки на интервалах, нанесенных на числовую прямую. Отметим на числовой прямой точки, как показано на рисунке:
 
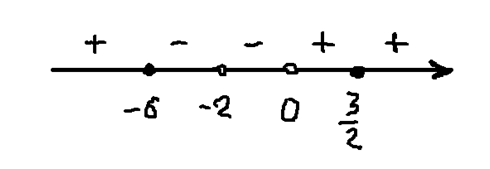
Эти точки являются границами интервалов, обозначающих множество решения нашего неравенства. При этом, точки -6 и 3/2 входят в множество решений, а точки -2 и 0 не входят.
Учитывая полученное выше неравенство \(x ≤ -{ 3\over2}\)  запишем решение неравенства:
 
 
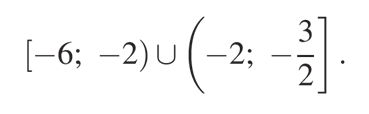
Автор - Андрей Найденов
 
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Наталья Николаевна Шарапова
Репетитор по математике
Стаж (лет)
21
Образование:
Челябинский государственный университет
Проведенных занятий:
152
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике с 1 по 9 класс. Подготовка к ОГЭ. Репетитор по информатике для 7-9 классов. Люблю математику и информатику, потому что просто люблю. Если бывает трудно, то предлагаю идти вместе. Когда человек не один, то всегда легче и интереснее. Заодно и вспомним, что забыл и выясним, что не знал. До встречи!
Мария Иванова Мозина
Репетитор по математике
Стаж (лет)
25
Образование:
Омский государственный педагогический университет
Проведенных занятий:
427
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Использую классическую методику преподавания. Мои ученики получают высокие балы по ОГЭ. Индивидуально подхожу к объяснению материала, выбираю доступные способы обучения, использую приемы соответственно возрасту и интересам ребенка. Добиваюсь полного понимания изучаемого материала. Прививаю и поддерживаю интерес детей к предмету.
Анна Фёдоровна Ринкман
Репетитор по математике
Стаж (лет)
30
Образование:
Коми государственный педагогический институт
Проведенных занятий:
133
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 1-4 классов и русскому языку 1-6 классов. Помогаю дошкольникам и ученикам младшей школы легко и доступно понять учебный материал. Работала по программе Л. Г. Петерсон. Терпеливо и творчески нахожу подход к каждому ученику.
Похожие статьи