Как легко разделить на 0,1; 0,01; 0,001

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Часто задаваемые вопросы:

Обновлено: 03 дек 2023

Как легко разделить на 0,1; 0,01; 0,001

Как быстрее разделить число (десятичную дробь) на \(0,1\); \(0,01\); \(0,001\) и т.д.? Для этого тебе даже не понадобиться калькулятор, изучите правило деления десятичных дробей на 0,1.

\(0,1-\) это десятичная дробь приведём её к виду обыкновенной дроби:

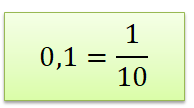
То есть деление на \(0,1\) можно заменить делению на \(\frac{1}{10}\), а при делении на \(\frac{1}{10}\) , мы меняет местами числитель и знаменатель. Число обратное \(\frac{1}{10}-\) это \(10.\) Чтобы разделить на \(0,1\) , надо число умножить на \(10.\) Легко не так ли?

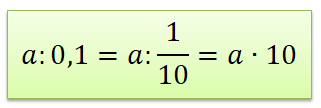
Аналогичное правило и для \(0,01\): при деление на \(0,01\) можно заменить делению на \(\frac{1}{100}\), а при делении на \(\frac{1}{100}\) мы меняет местами числитель и знаменатель. Чтобы разделить на \(0,01\) надо число умножить на \(100\).

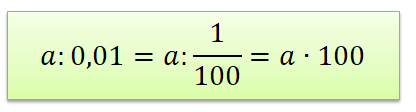
Аналогичное правило и для \(0,001\): при деление на \(0,001\) можно заменить делению на \(\frac{1}{1000}\), а при делении на \(\frac{1}{1000}\) мы меняет местами числитель и знаменатель. То есть для того чтобы разделить на \(0,001\) надо число умножить на \(1000\).

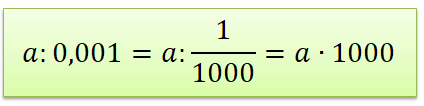
Пример 1. Разделите \(15\) на \(0,1\).

Решение: \(15:0,1=15:\frac{1}{10}=15*10=150\)

Ответ: \(150\).

Пример 2. Разделите \(25\) на \(0,01\).

Решение: \(25:0,01=25:\frac{1}{100}=25*100=2500\)

Ответ: \(2500\).

Пример 3. Разделите \(5\) на \(0,001\).

Решение: \(5:0,001=5:\frac{1}{1000}=5*1000=5000\)

Ответ: \(5000\).

Выводы:

Деление на 0,1 можно заменить делению на 1/10, а при делении на 1/10, дробь меняет местами числитель и знаменатель. Число обратное 1/10 это 10. Чтобы разделить на 0,1, надо умножить на 10. Аналогично и для 0,01: чтобы разделить на 0,01, надо умножить на 100.

Часто задаваемые вопросы:

✅ Можно ли поделить десятичную дробь на 0,1?

↪ Да, деление десятичной дроби на 0,1 эквивалентно умножению десятичной дроби на 10. Это связано с тем, что 0,1 является десятичной дробью, которая представляет десятую долю целого числа.

✅ Как выполняется деление десятичной дроби на 0,1?

↪ Чтобы разделить десятичную дробь на 0,1, достаточно переместить запятую в исходной дроби на одну позицию вправо. Например, если у нас есть десятичная дробь 0,35, то ее деление на 0,1 будет равно 3,5. Это происходит потому, что перемещение запятой вправо на одну позицию эквивалентно умножению на 10.

✅ Каково значение десятичной дроби после деления на 0,1?

↪ Значение десятичной дроби после деления на 0,1 будет равно исходному числу, увеличенному в 10 раз. Например, если исходная десятичная дробь равна 0,45, то после деления на 0,1 она станет равной 4,5. Это происходит потому, что деление на 0,1 эквивалентно умножению на 10, что приводит к увеличению значения десятичной дроби.

Предыдущая статья