• Альфашкола
  • Статьи
  • Как записать комплексное число в алгебраической и тригонометрической форме

Как записать комплексное число в алгебраической и тригонометрической форме

Дарим в подарок бесплатный вводный урок!

Предметы
Специализации
Комплесное число имеет три формы записи: алгебраическую, показательную и тригонометрическую. Проиллюстрируем на примере методы записи комплексного числа в алгебраической и тригонометрической форме и их использование для решения уравнений.    
 
Дано комплексное число z. Требуется:
  1. записать число z в алгебраической и тригонометрической формах;
  2. найти все корни уравнения \(ɷ^3-z=0\)
                                                         \({z}={{-2{\sqrt2}}\over1+i}\)
Решение:
1) Комплексное число z в алгебраической форме имеет вид: z=а+bi;
 в тригонометрической форме: z=r(cosj+i×sinj), где и r=\({ \sqrt{a^2+b^2}}\) и j=\(arctg {b \over a}\)
Для тог чтобы записать \({z}={{-2{\sqrt2}}\over1+i}\) в алгебраической форме, умножим числитель и знаменатель на сопряженное к знаменателю, т. е. на 1- i.
.
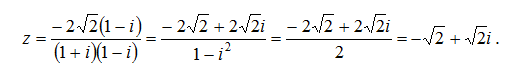
 \(z=-{\sqrt2}+{\sqrt2}i\)- алгебраическая форма.
 
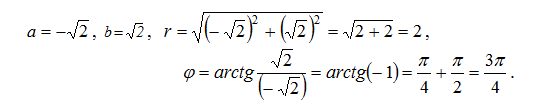
\(z=2{(cos{3π\over4}}+i sin{{3π\over4}})\)- тригонометрическая форма.
 
 
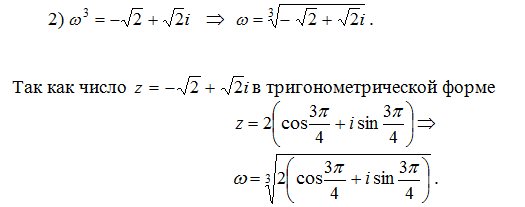
Применяя формулу для извлечения корня из комплексного числа:
 
Автор: Дмитрий Айстраханов
 
Больше уроков и заданий по всем школьным предметам в онлайн-школе "Альфа". Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Амаяк Варданович Варданян
Репетитор по математике
Стаж (лет)
6
Образование:
Российский университет дружбы народов
Проведенных занятий:
532
Форма обучения:
Дистанционно (Скайп)
Павел Андреевич Демин
Репетитор по математике
Стаж (лет)
4
Образование:
Южно-Уральский государственный гуманитарно-педагогический университет
Проведенных занятий:
103
Форма обучения:
Дистанционно (Скайп)
Алексей Сергеевич Макейчик
Репетитор по математике
Стаж (лет)
5
Образование:
БГЭУ
Проведенных занятий:
4450
Форма обучения:
Дистанционно (Скайп)
Похожие статьи