Как определить объем пирамиды

Математика Подготовка к ЕГЭ ЕГЭ по математике ОГЭ по математике Подготовка к ОГЭ

Пирамида (др.-греч. πυραμίς, πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.

Далее расскажем несколько способов, как найти объем треугольной пирамиды.

Лемма

Две пирамиды, имеющие равные высоты и равновеликие основания, имеют равные объемы.

Теорема

Объем пирамиды равен одной трети произведения площади основания на высоту.

Формула объема пирамиды: \(V={1\over3}S*H\) , где S – площадь основания, H – высота пирамиды.

Теорема

Объем V усеченной пирамиды может быть найден по формуле \(V={1\over3}H(S1+{{\sqrt {S1S2}}}+S2)\), где H – высота усеченной пирамиды, S1 и S2 – площади ее оснований.

Часто даны координаты вершин пирамиды ABCD и требуется найти ее объем. Даная задача может быть решена методами аналитической геометрии. Покажем ее решение на примере.

Пусть даны координаты вершин пирамиды ABCD и требуется найти ее объем: A(10;6;6), B(-2;8;2), C(6;8;9), D(7;10;3).

Решение

Объем пирамиды равен \(1\over6\) объема параллелепипеда, построенного на векторах AB, AC, AD. Найдем координаты этих векторов, для этого из соответствующей координаты конца вектора вычтем координату его начала:

AB=(-12;2;-4), AC=(-4;2:3), AD=(-3;4;-3).

Тогда объем параллелепипеда равен значению детерминанта (определителя) матрицы, составленной из координат векторов (строка матрицы – координаты вектора). Определитель третьего порядка находим по правилу треугольников.

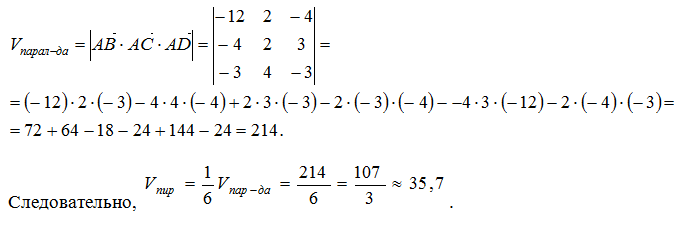
Автор - Дмитрий Айстраханов

Часто задаваемые вопросы

Можно ли использовать эту формулу для любой пирамиды?

Да, эту формулу можно использовать для любой пирамиды, независимо от формы её основания, при условии, что вы знаете площадь основания и перпендикулярную высоту пирамиды.

Как найти площадь основания пирамиды?

Это зависит от формы основания. Если основание — это квадрат, то площадь равна �2a2 (где �a — сторона квадрата). Если основание — это треугольник, то используйте соответствующую формулу для вычисления площади треугольника, и так далее.

Предыдущая статья

Следующая статья

Дарим в подарок бесплатный вводный урок!

Как определить объем пирамиды

Часто задаваемые вопросы

Дарим в подарок бесплатный вводный урок!

Репетиторы

Специализация

Похожие статьи