С 10 до 22.00 по МСК ежедневно

>Записаться на урок

Скорость сближения и скорость удаления

Дарим в подарок бесплатный вводный урок!

Предметы
Специализации
В математике целый пласт задач о том, как найти скорость сближения и удаления (при встречном движении, в одном направлении или в противоположных направлениях).
В этой статье расскажем, как решать задачи на скорость сближения и удаления (4 класс).
 
Для решения задач на движение стоит прояснить объекты сближаются или удаляются, ответ зависит от вида движения.  Когда объекты двигаются навстречу друг другу из разных пунктов, то они сближаются:
Скорость сближения: формула
\(v_1+v_2=20+30=50\) км/час
Когда объекты двигаются в противоположных направлениях  из одного пункта, то они удаляются:
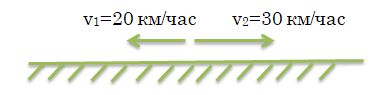
Скорость удаления: формула
 
\(v_1+v_2=20+30=50\) км/час
 
 
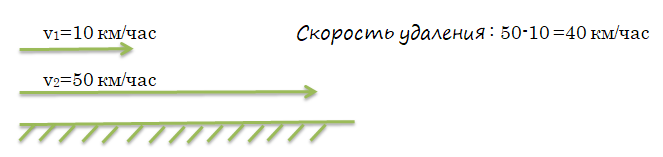
Когда объекты двигаются в одном направление одновременно:
  • Если они выезжают одновременно, то два объекта удаляются друг от друга, так как скорость у них разная, для того чтобы найти скорость их удаления надо из большей скорости вычесть меньшую.
\(v_y=v_2-v_1\)
Движение в одном направлении
 
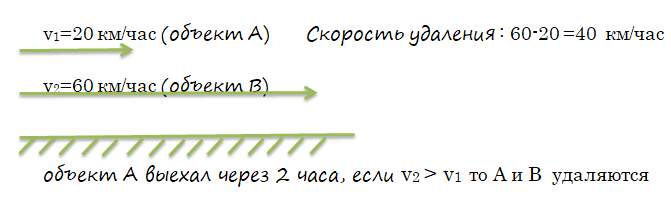
  • Если они выезжают с интервалом, то два объекта могут удаляться или сближаться в зависимости от их скоростей:
1) если скорость объекта, который впереди больше, то они удаляются.  \(v_2>v_1\) 
Движение в одном направлении
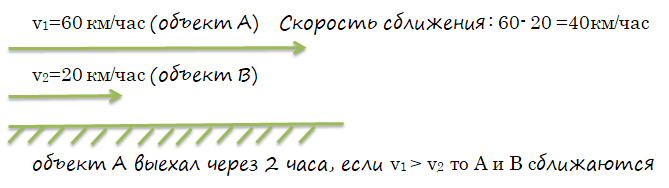
                                                        2) если скорость объекта, который впереди меньше, то они сближаются .  \(v_1>v_2\)
Движение в одном направлении

Часто задаваемые вопросы:

↪ Если два объекта движутся навстречу друг другу со скоростями 1v1 и 2v2, их общая скорость сближения равна v1+v2.

↪ Если один объект движется быстрее другого со скоростями v1 и v2 (где v1>v2), их общая скорость удаления равна v1−v2.

Больше уроков и заданий по всем школьным предметам в онлайн-школе "Альфа". Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку "Записаться" принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Жанна Игоревна Стефанович
Репетитор по математике
Стаж (лет)
20
Образование:
Гродненский государственный университет им. Янки Купалы
Проведенных занятий:
116
Форма обучения:
Дистанционно (Скайп)
Наталия Дмитриевна Мацак
Репетитор по математике
Стаж (лет)
30
Образование:
Кубанский государственный университет
Проведенных занятий:
830
Форма обучения:
Дистанционно (Скайп)
Аурика Витальевна Чуева
Репетитор по математике
Стаж (лет)
24
Образование:
ГОУ
Проведенных занятий:
188
Форма обучения:
Дистанционно (Скайп)
Похожие статьи