Как по заданным функции, точке и вектору вычислить градиент в точке и производную функции в точке по направлению вектора

Все Родителям Саморазвитие для школьников Подготовка Преподавателям Профориентация Отношения с родителями Советы психолога Здоровье Таймменеджмент Калькуляторы

Как найти градиент функции
Часто задаваемые вопросы:

20 июл 2024

Как по заданным функции, точке и вектору вычислить градиент в точке и производную функции в точке по направлению вектора

Часто попадается задача, где нужно найти производную функции в точке по направлению вектора, найти градиент функции и производную модуля. Давайте разберем на примере.

Даны функция

Вычислить:

б) производную функции z в точке А по направлению вектора а.

Решение

а) Находим частные производные функции z в общем виде:

Значения этих величин в точке А:

Градиент определяем по формуле:

б) Определяем модуль этого вектора:

Отсюда получаем значения направляющих косинусов вектора а:

Значение производной заданной функции по направлению вектора а определяем по формуле:

Окончательно получаем:

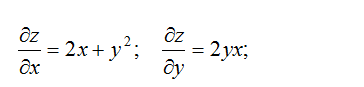
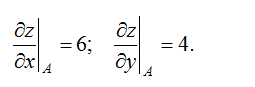
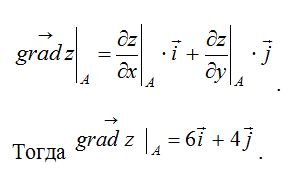
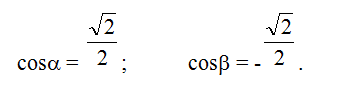
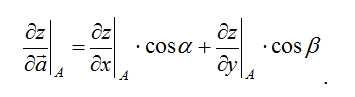
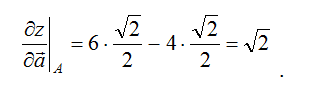
Как найти градиент функции

Для нахождения градиента функции нужно вычислить ее частные производные по каждой переменной и объединить их в вектор. Вот шаги для нахождения градиента функции:

Запишите функцию, для которой нужно найти градиент. Предположим, у нас есть функция f(x, y) с двумя переменными x и y.
Вычислите частные производные функции f(x, y) по каждой переменной. Для этого возьмите производную функции по одной переменной, считая все остальные переменные константами.
Представьте частные производные в виде вектора. Градиент функции будет вектором, где каждая компонента соответствует частной производной по соответствующей переменной. Например, если частная производная по x равна ∂f/∂x, а по y - ∂f/∂y, то градиент будет вектором (∂f/∂x, ∂f/∂y).
Готово! Вы получили градиент функции.

Градиент функции является вектором, указывающим направление наибольшего возрастания функции в каждой точке. Он также может использоваться в оптимизации функций и векторном анализе.

Часто задаваемые вопросы:

✅ Что такое градиент функции и какую роль он играет?

↪ Градиент функции - это вектор, состоящий из частных производных функции по каждой переменной. Он указывает направление наибольшего возрастания функции в каждой точке и используется в оптимизации функций и векторном анализе.

✅ Как найти градиент функции с несколькими переменными?

↪ Для нахождения градиента функции с несколькими переменными необходимо вычислить частные производные функции по каждой переменной и объединить их в вектор. Градиент будет вектором, где каждая компонента соответствует частной производной по соответствующей переменной.

✅ Как интерпретировать значения градиента функции?

↪ Значения градиента функции указывают направление наибольшего возрастания функции в каждой точке. Вектор градиента будет перпендикулярен поверхности функции в данной точке, а его длина будет показывать скорость изменения функции в этом направлении. Большие значения градиента указывают на более крутой рост функции, а нулевой градиент указывает на экстремум или плато функции.

Предыдущая статья