Дарим первый урок с репетитором бесплатно
Оставьте заявку и получите первый урок в подарок



Как найти точку пересечения плоскости и прямой
1. Найти точку пересечения плоскости \(x-2y+3z-8=0\) с прямой, заданной общими уравнениями:
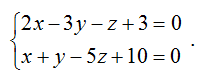 .
.Решение сводится к решению системы трех уравнений с тремя неизвестными:

2. Найти точку пересечения плоскости \(x+y+3z-1=0\) с прямой, заданной каноническими уравнениями:
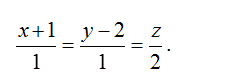
Можно было бы перейти от канонических уравнений к общему виду и свести задачу к рассмотренной в предыдущем примере. Но можно рассуждать и по-другому. Точка пересечения должна принадлежать и прямой, и плоскости, то есть можно подставить выражения для x,y и z из канонического уравнения в уравнение плоскости и определить их.
1) Перейдем к параметрическим уравнениям прямой:
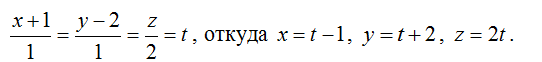
2) Подставим найденные выражения в уравнение плоскости:
\((t-1)+(t+2)+3*2t-1=0\), откуда t=0
3) Подставляем в выражения для x,y,z, находим ответ: x=-1, y=2, z=0.
Ответ: искомая точка M(-1;2;0).
Дарим в подарок бесплатный вводный урок!


Репетиторы

Специализация

-
 Подготовка к ЕГЭ по математике базовый уровень
Подготовка к ЕГЭ по математике базовый уровень -
 Репетитор для подготовки к ОГЭ по физике
Репетитор для подготовки к ОГЭ по физике -
 Подготовка к олимпиадам по физике
Подготовка к олимпиадам по физике -
 Репетитор ЕГЭ по английскому
Репетитор ЕГЭ по английскому -
 Репетитор по английскому с нуля
Репетитор по английскому с нуля -
 Репетитор по грамматике английского языка
Репетитор по грамматике английского языка -
 Репетитор по разговорному английскому
Репетитор по разговорному английскому -
 ВПР по физике
ВПР по физике -
 Подготовка к ЕГЭ по биологии онлайн
Подготовка к ЕГЭ по биологии онлайн -
 Подготовка к ЕГЭ по информатике
Подготовка к ЕГЭ по информатике


 О платформе
О платформе  Премиум математика
Премиум математика  Репетиторы
Репетиторы  Тарифы
Тарифы  Вход
Вход

