Как написать каноническое и параметрическое уравнение прямой, образованной пересечением плоскостей
Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей
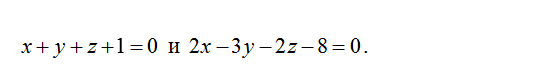
Решение
1) Найдем координаты фиксированной точки. Из исходной системы уравнений
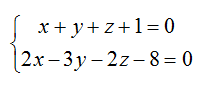
исключим z.
Положим z=0, тогда:
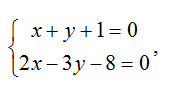
откуда находим: x=1, y= -2.
Таким образом, нашли координаты фиксированной точки M0(1,-2,0).
2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:
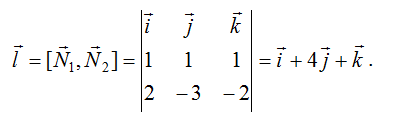
3) Запишем канонические уравнения:
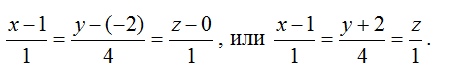
4) Обозначив,
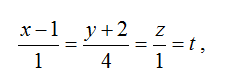
получаем параметрические уравнения:
x=t+1, y=4t-2, z=4
Наши преподаватели
Репетитор по математике
Стаж (лет)
1
Образование:
Тюменский государственный университет
Проведенных занятий:
37
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
26
Образование:
Омский государственный педагогический университет
Проведенных занятий:
593
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике
Стаж (лет)
29
Образование:
Калужский государственный педагогический институт им. К.Э. Циолковского
Проведенных занятий:
48
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по олимпиадной математике
- Репетитор по химии для подготовки к ОГЭ
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Английский язык для начинающих
- Репетитор по английскому для взрослых
- ВПР по математике
- Репетитор для подготовки к ВПР по русскому языку
- Репетитор по информатике для подготовки к ЕГЭ
- Подготовка к ОГЭ по литературе
Похожие статьи
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так